Given the line with parametric equation r = a + d show that the perpendicular distance p from the origin to this line can take

Given the line with parametric equation r = a + λd show that the perpendicular distance p from the origin to this line can take either of the forms

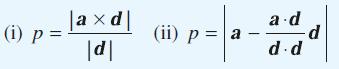
Find the parametric equation of the straight line through the points A(1, 0, 2) and B(2, 3, 0) and determine

(a) The length of the perpendicular from the origin to the line;

(b) The point at which the line intersects the y–z plane;

(c) The coordinates of the foot of the perpendicular to the line from the point (1, 1, 1).