Question: Prove that if g(x) is an odd function and f(x) an even function of x, the product g(x)[c + f(x)] is an odd function if

Prove that if g(x) is an odd function and f(x) an even function of x, the product g(x)[c + f(x)] is an odd function if c is a constant. A periodic function with period 2π is defined by

in the interval –π ≤ θ ≤ π. Show that the Fourier series representation of the function is

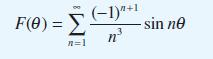
F(0) = (-1)+1 n n=1 sin no

F(0) = 20(0)

Step by Step Solution

★★★★★

3.41 Rating (157 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

gx c fx cgx gxfx cgx cgxfx from the given information gx c fx Thus the product is an ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Engineering Mathematics Questions!

Corporate Venture Capital at Eli Lilly Read the case study and answer the following questions: What is the role of corporate venture capital? What is your assessment of Lilly Ventures? What should...

Use the guidelines of Section 4.5 to sketch the curve. y = sin 2 x 2 cos x Data from section 4.5 GUIDELINES FOR SKETCHING A CURVE The following checklist is intended as a guide to sketching a curve...

1. Given the functions x) = x2 + 1 and g(x) = 3 - x, determine an equation for the combined function y =x) + gx). a. y=x3x+2 b. y=x2+x+4 c.y=x3x+4 d. y=x2+x2 2. Iff= {('?, 1), (5, 8),(3, 11), (5,l)}...

8. If x) is an odd function and g(x) is an even function, then what type of function is y = x) + g(x)? a. odd b. even c. neither d. cannot be determined for sure 9. If x) and ng) are even functions,...

THE CHAIN RULE If g is differentiable at x and f is differentiable at g x then the composite function F f g defined by F x f g x is differentiable at x and F is given by the product F x f g x g x In...

Which comparison is correct for the values of f a and g x when x 1 Function A f x x 1 Function B X 3 1 0 2 o f 1 g 1 Of 1 g 1 9 x 7 4 1 2

6 Complete the table Show your work You can write the vertex you found from Problem 2 a f x 21 21 3 b g x 3x 2 c Function d f x 1 3 h z 3r Vertex Vertical Intercept Vertex 7 For each quadratic...

[Q1] [20 points] You can leave answers unsimplified. (A) How many lists of length 5 can be made from the letters A, B, C, D, E, F, G. H if repetition is allowed? (B) How many lists of length 5 can be...

How does the boiling process at supercritical pressures differ from the boiling process at sub critical pressures?

brandlin company of anaheim, california, sells parts to a foreign customer on december 1, 2017, with payment of 28000 koruna reg a1 reg a2 to a4 reg b1 reg b2 to b4 a2 what is the impact on 2017 net...

Long - term capital gains are taxed at rate of: 0 % 1 5 % 2 0 % it depends on the taxpayer's ordinary income tax rate.

3. What is product diversification?

Determine the support reactions at and . Take E = 200 MPa, I = 300(10 6 ) mm 4 , A = 21(10 3 ) mm 2 for each member. - 5 m 300 kN m, 3 9. (2, 4 m 2

Determine the structure stiffness matrix K for the frame. Take E = GPa, I = 350(10 6 ) mm 4 , A = 15(10 3 ) mm 2 for each member. Joints at and are pins. 2 60 kN 3 |1 2) 2 m - - 2 m 2 4 m

Determine the support reactions at pins and . Take E = 200 GPa, I = 350(10 6 ) mm 4 , A = 15(10 3 ) mm 2 for each member. 2 60 kN 3 - 2 m 2 m 4 m 3) 9

3. You want to retire in 15 years with $2.5 million. How much would you have to invest quarterly at a 9.5% interest rate to reach your goal?

Q2. How might an Integrated Enterprise System and Business Intelligence create more value for an enterprise?

Hamilton Investments has recently began trading on the stock exchange after issuing 80 million shares sold at an initial subscription price of $2.85 each. Of this subscription price the company...