Question: Show that the matrix has eigenvalues 5, 3, 3. Find the corresponding eigenvectors. For the repeated eigenvalue, show that it has two linearly independent eigenvectors

Show that the matrix

-2 2-3] A = 2 1 -6 -1 -2 0

has eigenvalues 5, –3, –3. Find the corresponding eigenvectors. For the repeated eigenvalue, show that it has two linearly independent eigenvectors and that any vector of the general form

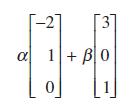
0 -2 3 1 + B 0 0

is also an eigenvector.

Step by Step Solution

★★★★★

3.40 Rating (163 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

A3221145 3 3 50 x 2 3 x 6 y Eac... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Engineering Mathematics Questions!

The phase portraits in Problems 17 through 28 correspond to linear systems of the form x' = Ax in which the matrix A has two linearly independent eigenvectors. Determine the nature of the eigenvalues...

Can you please help me with number 31. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials and Linear...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

Can you please help me with number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! Linear Systems quations 406 The...

4. (a) A social club has a lucky draw every weekend in which the chance of winning a prize is 25%. Suppose that 0 Anyone who won a prize last week is not eligible for this week's draw; they enter the...

Show all work Problem 5 [12 marks ]: Let A be the (4 x4)-matrix displayed in cells 620-J23 of the Excel spreadsheet. Moreover, let to be the length 4 column vector displayed in cells 627-630. Use...

This is a Linear Algebra Question. Both the QUESTION and SOLUTION are shown below: I only have a question regarding part b). I have included part a) for clarity. Question regarding RED underlined...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials...

Suppose credit rating is the only thing that determines companies' debt interest rate. Below is the interest rate associated with each credit rating. Credit rating Interest rate AAA AA A BBB BB 3.5%...

Calculate the percentage by mass of oxygen in the following compounds: (a) Morphine, C17H19NO3 (b) Codeine, C18H21NO3 (c) Cocaine, C17H21NO4 (d) Tetracycline, C22H24N2O8 (e) Digitoxin, C41H64O13 (f)...

CHALLENGE Health benefits of bee pollen. Bee pollen is effective for combating fatigue, depression, cancer, and colon disorders. So says a Web site that offers the pollen for sale. We wonder if bee...

Government Identify one federal department or agency that provides assistance or support to businesses in the areas of risk assessment and risk management. Write a short report that describes the...

Starting with benzene and any reagents with three or fewer carbon atoms, show how you would prepare each of the following compounds: (a) (b) (c) (d) Z NH2 CI .CI I

How would you use NMR spectroscopy to distinguish between the following pairs of compounds? (a) (b) 'N. 'N- N.

Spermine is a naturally occurring compound that contributes to the characteristic odor of semen. Classify each nitrogen atom in spermine as primary, secondary, or tertiary. NH2 H,N 'N' Spermine

Cedric Company recently traded in an older model computer for a new model. The old models book value was $323,000 (original cost of $673,000 less $350,000 in accumulated depreciation) and its fair...

An IC needs to be insulated, with three different plastic materials, which have different thermal conductivity which are ka-3, k-1 and k = 0.2, all with British units and going from outside to inside...

Figure 6-12 Twinnings Corporation manufactures Scheduling Books. There are two processes: printing and binding. The following information is given for the printing department for September. (The...