The function A() is as given by (10.55) and shown in Figure 10.27. Show that A() has a simple maximum point when max. Find

The function A(Ω) is as given by (10.55) and shown in Figure 10.27. Show that A(Ω) has a simple maximum point when ζ max. Find Ω_max as a function of ζ and ω , and also find A(Ω_max).

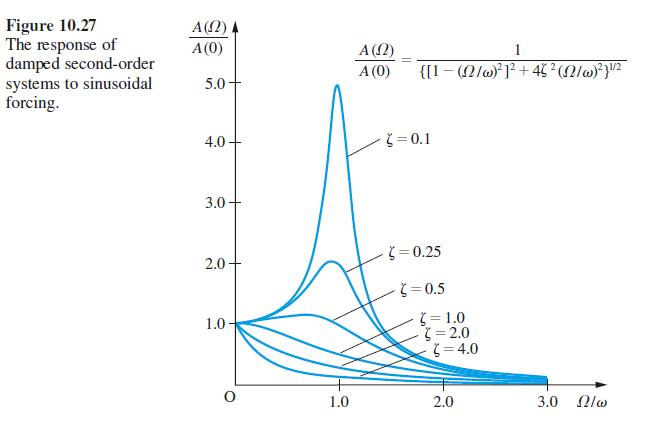
For >, A(2) has no maximum, but does have a single point of inflection. Show, by consideration of Figure 10.27, that |dA/d is a maximum at the point of inflection. Let , be the value of 2 for which the point of inflection occurs. Show that satisfies the equation 326 +5Bw+ + (4B - 3)w2 Bw = 0 where 3 = 2 - 1. Hence show that for ( = 2/2 the greatest value of |dA/d2 occurs when = w and is 1/(2w). Also find the greatest values of |dA/d when = (+3) and when ( = 1.