We discussed the process of numerical differentiation using the approximation Using the Taylor series for f(a h) and f(a h) about x a, show that to f(a) with truncation error O(h 6 ) Apply this extrapolation procedure to find f(1) when f(x) cosh x, taking h 0 4, 0 2 and 0 1, working to as many decimal places as your calculator will permit o(h) f(a h) f(a h) 2h

Question: We discussed the process of numerical differentiation using the approximation Using the Taylor series for f(a + h) and f(a h) about x

We discussed the process of numerical differentiation using the approximation

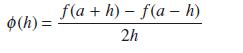
o(h) = f(a+h)-f(ah) 2h

Using the Taylor series for f(a + h) and f(a – h) about x = a, show that

h+ f'(a) = $(h) - f (a)- 5f (a) - .. h 3! 5! and deduce that '(a) = } [40(h) o(h)] + +[(a) + . - Writing (h)

to f´(a) with truncation error O(h⁶). Apply this extrapolation procedure to find f´(1) when f(x) = cosh x, taking h = 0.4, 0.2 and 0.1, working to as many decimal places as your calculator will permit.

o(h) = f(a +h)-f(a - h) 2h

Step by Step Solution

★★★★★

3.40 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a h fa 1 a h h ah fa a ha 2 a 2h a h a h 2h a 1 3 a 6h h 7 3 a ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Modern Engineering Mathematics Questions!

For each of the following transactions, STATE the ledger accounts affected, and whether the ledger account should be debited or credited. You are NOT required to prepare T accounts. 1. Purchased...

Using the scores 2, 5, 8, 9, and 16, first find x and s, then replace each score by its corresponding z score. (Don't round the z scores; carry as many decimal places as your calculator can handle.)...

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

Consider the following function f x x a 5 points Approximate f by a Taylor polynomial T3 x with the center x 1 Your answer must be of the form co c x 1 c x 1 c x 1 b 5 points How good is the...

Please Help The Taylor series for f (ac ) = ac at -3 is Cn ( 2 + 3 ) " . n=0 Find the first few coefficients. CO = C1 = C2 = C3 C4The Maclaurin series of the function x) 2 5:3 tan1 (91:2) 00 can be...

Please help to solve these Please let me know in the comments what additional things you need because there is nothing else I have to add. These are just calculus problems. The Taylor series for f...

7. Complete the table of derivatives for f (x) = sin (x] cos(x) (use technology to help find the derivatives). Write out the first few non-zero terms of the series to help you find a pattern, then...

626 CHAPTER 8 INFINITE SEQUENCES AND SERIES CAS 9-10 Use a computer algebra system to find the Taylor poly- 26. Suppose you know that nomials 7, centered at a for n = 2, 3, 4. 5. Then graph these...

3. Consider the function f : R\\ {-3} - R : IH x +3 (a) Determine the general expression for f(")(x), i.e., the formula of the n-th derivative of f, for n > 1. Prove that this expression is correct....

For this Performance Task, imagine that the deputy mayor of your city contacts you to arrange a meeting to discuss how to reduce the number of inmates in local jails and prisons due to overcrowding....

Q2. C. Develop a requirements traceability matrix (RTM) for your own class group project showing three items with different categories (write your project name and group in the above of the table)?...

Pugh accounts for treasury stock under the cost method. Laws in the state of Pugh's incorporation protect shares held in treasury from dilution when stock dividends or stock splits are declared. In...

(a) ... corporate planning and budgetmg are complementary, rather than the former superseding the latter. Compare the aims and main features of 'corporate planning' and 'budgeting' systems. (12...

The stressstrain diagram for a titanium alloy can be approximated by the two straight lines. If a strut made of this material is subjected to bending, determine the moment resisted by the strut if...

The Plexiglas bar has a stressstrain curve that can be approximated by the straight-line segments shown. Determine the largest moment M that can be applied to the bar before it fails. (MPa) 20 mm...

The beam is made of an elastic perfectly plastic material for which Ï Y = 250 MPa. Determine the residual stress in the beam at its top and bottom after the plastic moment M p is applied and...

On December 2, Coley Corp. acquired 1,600 shares of its $5 par value common stock for $21 each. On December 20, Coley Corp. reissued 1,200 shares for $14 each. Which of the following is correct...

QUESTION 1 Which of the following can be considered heuristic for a good user - interface design? A . c nsistency B . flexibility C . recognition rather than recall D . all of the above

Fargo company established a $250 petty cash fund on March 1 of this year. On March 22, the fund showed $155 in cash, and receipts for the following expenditures: $32 postage, $48 gasoline expenses,...