Chebyshev’s inequality, introduced in Chapter 3 Exercise 45, is valid for continuous as well as discrete distributions. It states that for any number k ≥ 1, P(lX – μl ≥kσ) ≤ 1/k² (see the aforementioned exercise for an interpretation and Chapter 3 Exercise 163 for a proof). Obtain this probability in the case of a normal distribution for k = 1, 2, and 3, and compare to the Chebyshev upper bound.

Data From Chapter 3 Exercise 45

Data From Exercise 163 in Chapter  3

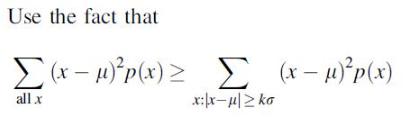
A result called Chebyshev's inequality states that for any probability distribution of a rv X and any number k that is at least 1, P(|X-u ko) 1/k. In words, the probability that the value of X lies at least k standard deviations from its mean is at most 1/k.