Consider spacetime paths between fixed endpoints (A) and (B). For a Lagrangian function (Lleft(x^{mu}(sigma), dot{x}^{mu}(sigma) ight)), where (sigma) parameterizes the position on the path and

Consider spacetime paths between fixed endpoints \(A\) and \(B\). For a Lagrangian function \(L\left(x^{\mu}(\sigma), \dot{x}^{\mu}(\sigma)\right)\), where \(\sigma\) parameterizes the position on the path and \(\dot{x}^{\mu} \equiv d x^{\mu} / d \sigma\), define an integral over a path

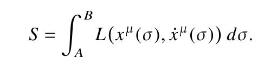
Show that for an arbitrary small variation in the path \(x^{\mu}(\sigma) \rightarrow x^{\mu}(\sigma)+\delta x^{\mu}(\sigma)\), the corresponding variation in the value of the integral is

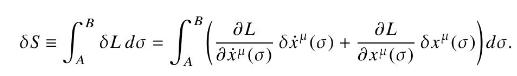
Integrate this by parts and use that the variation vanishes at the endpoints (by definition) to show that this leads to the Euler-Lagrange equations (16.14). Thus show that the variational condition \(\delta S=0\) (Hamilton's principle) is equivalent to satisfaction of the Euler-Lagrange equations.

S = B = S A L(x" (0), x" (o)) do.