Consider scattering by a repulsive -shell potential: (a) Set up an equation that determines the s-wave phase shift 0 as a function of k(E

Consider scattering by a repulsive δ-shell potential: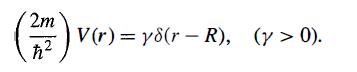

(a) Set up an equation that determines the s-wave phase shift δ₀ as a function of k(E = h̄²k² /2m).

(b) Assume now that γ is very large,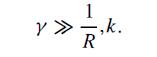

Show that if tan kR is not close to zero, the s-wave phase shift resembles the hard-sphere result discussed in the text. Show also that for tan kR close to (but not exactly equal to) zero, resonance behavior is possible; that is, cotδ₀ goes through zero from the positive side as k increases. Determine approximately the positions of the resonances keeping terms of order 1/ γ; compare them with the bound-state energies for a particle confined inside a spherical wall of the same radius,

Also obtain an approximate expression for the resonance width Г defined by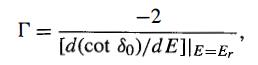

and notice, in particular, that the resonances become extremely sharp as γ becomes large.

2m V(r)= y8(r-R), (y > 0).