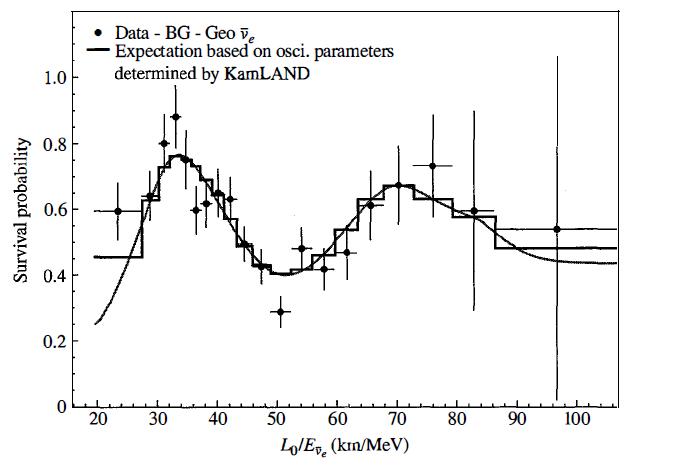
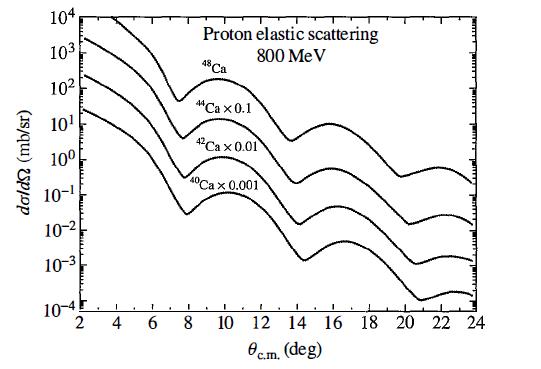
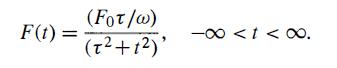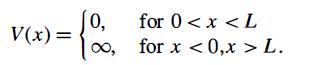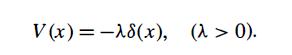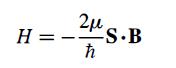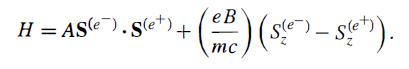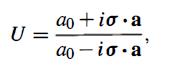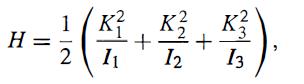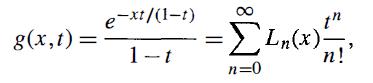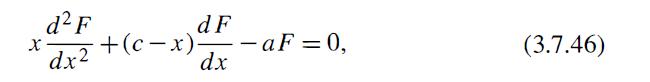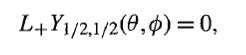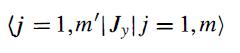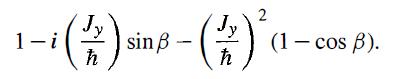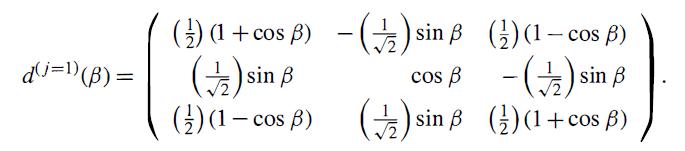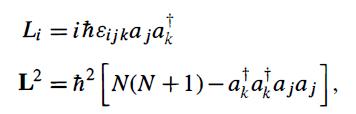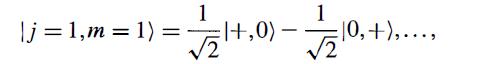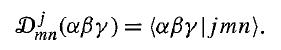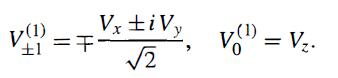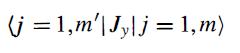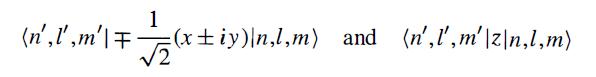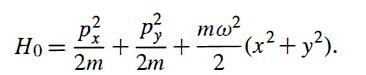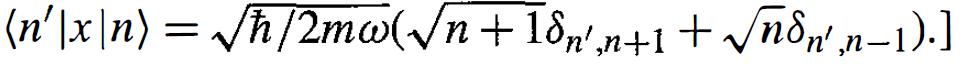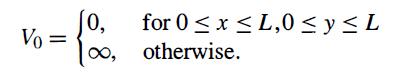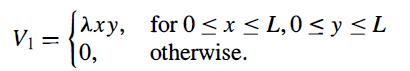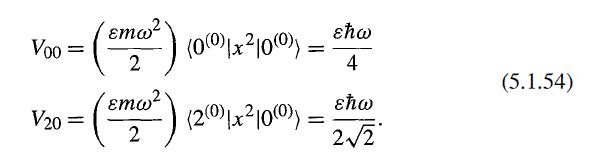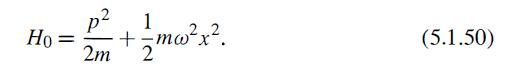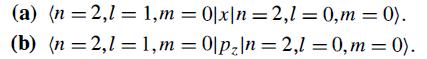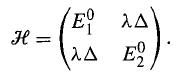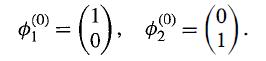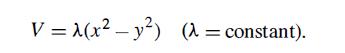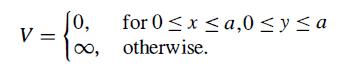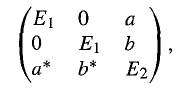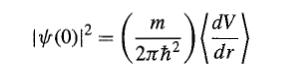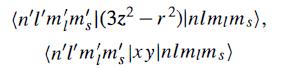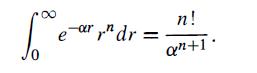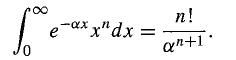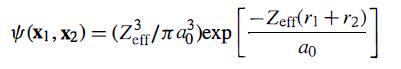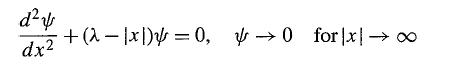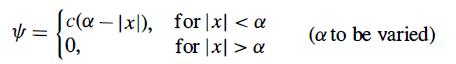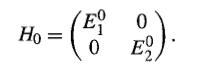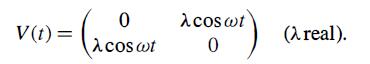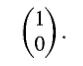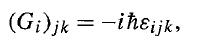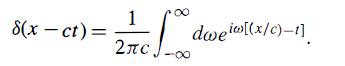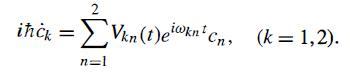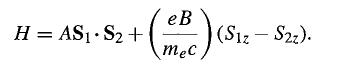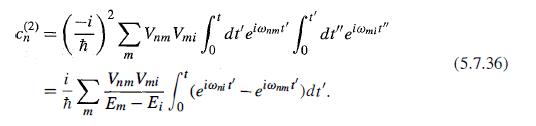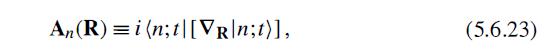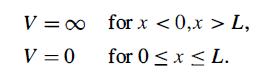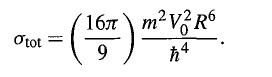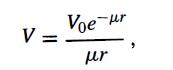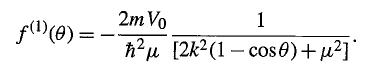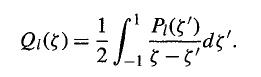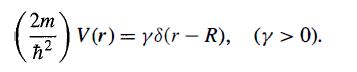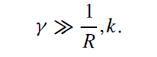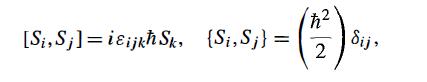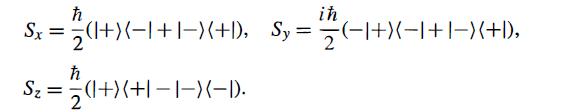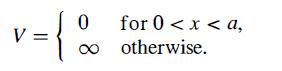Modern Quantum Mechanics 2nd Edition J. J. Sakurai, Jim J. Napolitano - Solutions

Unlock the complete understanding of "Modern Quantum Mechanics 2nd Edition" by J. J. Sakurai and Jim J. Napolitano with our comprehensive resources. Access online solutions and answers key that are designed to assist with the textbook's challenging questions. Our solution manual offers step-by-step answers and solved problems, perfect for students and instructors alike. Download chapter solutions in PDF format for convenient study, or explore our test bank for a variety of questions and answers. Whether you need an instructor manual or free downloads, our resources provide everything necessary to excel in quantum mechanics.

A one-dimensional simple harmonic oscillator of angular frequency ω is acted upon by a spatially uniform but time-dependent force (not potential)At t = -∞, the oscillator is known to be in the ground state. Using the timedependent perturbation theory to first order, calculate the probability
Derive the neutrino oscillation probability and use it, along with the data in Figure 2.2, to estimate the values of Δm2c4 (in units of eV2) and θ. Survival probability 1.0 0.8 0.6 0.4 0.2 0 - 20 Data - BG-Geo ve Expectation based on osci. parameters determined by KamLAND 30 40 50 60 70 Lo/Ev
A particle in one dimension is trapped between two rigid walls:At t = 0 it is known to b e exactly at x = L /2 with certainty. What are the relative probabilities for the particle to be found in various energy eigenstates? Write down the wave function for t ≥ 0. (You need not worry about absolute
An electron is subject to a uniform, time-independent magnetic field of strength B in the positive z-direction. At t = 0 the electron is known to be in an eigenstate of S • n̂ with eigenvalue h̄/2, where n̂ is a unit vector, lying in the xz-plane, that makes an angle β with the z-axis.(a)
Consider a particle in one dimension bound to a fixed center by a δ-function potential of the formFind the wave function and the binding energy of the ground state. Are there excited bound states? V(x)=-vod(x), (vo real and positive).
A particle of mass m in one dimension is bound to a fixed center by an attractive δ-function potential:At t = 0, the potential is suddenly switched off (that is, V = 0 for t > 0). Find the wave function for t > 0. (Be quantitative! But you need not attempt to evaluate an integral that may
Find, by explicit construction using Pauli matrices, the eigenvalues for the Hamiltonianfor a spin 1/2 particle in the presence of a magnetic field H = 2μ ħ S.B
The spin-dependent Hamiltonian of an electron positron system in the presence of a uniform magnetic field in the z-direction can be written asSuppose the spin function of the system is given by(a) Is this an eigenfunction of H in the limit A → 0, e B ⁄ mc ≠ 0? If it is, what is the energy
Consider the 2 x 2 matrix defined bywhere a0 is a real number and a is a three dimensional vector with real components.(a) Prove that U is unitary and unimodular.(b) In general, a 2 x 2 unitary unimodular matri x represents a rotation in three dimensions. Find the axis and angle of rotation
Consider a spin 1 particle. Evaluate the matrix elements of S₂(S₂+h)(S₂-ħ) and Sx(Sx+ħ)(Sx -ħ).
Let the Hamiltonian of a rigid body bewhere K is the angular momentum in the body frame. From this expression obtain the Heisenberg equation of motion for K, and then find Euler's equation of motion in the correspondence limit. H -1 (4+4+4). 2 13
Let U = eiG3αeiG2β eiG3γ, where (a ,β, γ) are the Eulerian angles. In order that U represent a rotation (a ,β, γ), what are the commutation rules that must be satisfied by the Gk? Relate G to the angular-momentum operators.
Follow these steps to show that solutions to Kummer's Equation (3.7.46) can be written in terms of Laguerre polynomials Ln (x ), which are defined according to a generating function aswhere 0 (a) Prove that Ln(0) = n ! and L0(x) = 1.(b) Differentiate g(x , t) with respect to x, show thatand find
Show that the orbital angular-momentum operator L commutes with both the operators p2 and x2; that is, prove (3.7.2). [L,p²] = [L,x²] = 0 (3.7.2)
Suppose a half-integer l-value, say 1/2, were allowed for orbital angular momentum. Fromwe may deduce, as usual,Now try to construct Y1/2,-1/2(θ,ϕ) by (a) applying L_ to Y1/2,-1/2(θ,ϕ); and (b) using L_ to Y1/2,-1/2(θ,ϕ) = 0. Show that the two procedures lead to contradictory results . (This
The wave function of a particle subjected to a spherically symmetrical potential V (r) is given by(a) Is Ψ an eigenfunction of L2? If so, what is the ! value? If not, what are the possible values of l that we may obtain when L2 is measured?(b) What are the probabilities for the particle to be
(a) Consider a system with j = 1. Explicitly writein 3 x 3 matrix form.(b) Show that for j = 1 only, it is legitimate to replace e-iJyβ/h̄ by(c) Using (b), prove (j = 1,m'Jy|j = 1,m)
The goal of this problem is to determine degenerate eigenstates of the threedimensional isotropic harmonic oscillator written as eigenstates of L2 and Lz, in terms of the Cartesian eigenstates |nxnynz) .(a) Show that the angular-momentum operators are given bywhere summation is implied over
We are to add angular momenta j1 = 1 and j2 = 1 to form j = 2, 1 , and 0 states. Using either the ladder operator method or the recursion relation, express all (nine) {j,m} eigenkets in terms of |j1j2;m1m2〉. Write your answer aswhere + and 0 stand for m1,2 = 1 , 0, respectively. \j = 1,m = 1)
Express the matrix elementin terms of a series in (α2β2γ2\J3|αιβιγι)
Consider a spherical tensor of rank 1 (that is, a vector)Using the expression for d(J=l) given in Problem 3.26, evaluateand show that your results are just what you expect from the transformation properties of Vx,y,z under rotations about the y-axis.Data from problem 3.26:Consider a system with j =
Consider a spinless particle bound to a fixed center by a central force potential.(a) Relate, as much as possible, the matrix elementsusing only the Wigner-Eckart theorem. Make sure to state under what conditions the matrix elements are nonvanishing.(b) Do the same problem using wave functions
(a) Write xy, xz, and (x2 - y2) as components of a spherical (irreducible) tensor of rank 2.(b) The expectation valueis known as the quadrupole moment. Evaluatewhere m′ = j, j - 1, j - 2, . . . , in terms of Q and appropriate Clebsch-Gordan coefficients. Q = ela, j,m=j|(3z² — r²)|a, j,m = j)
(a) Construct a spherical tensor of rank 1 out of two different vectors U = (Ux, Uy, Uz) and V = (Vx, Vy, Vz). Explicitly write T±(1)1,0 in terms of Ux,y,z and Vx,y,z.(b) Construct a spherical tensor of rank 2 out of two different vectors U and V. Write down explicitly T±2(2)±1,0 in terms
Consider an isotropic harmonic oscillator in two dimensions. The Hamiltonian is given by(a) What are the energies of the three lowest-lying states? Is there any degeneracy? (b) We now apply a perturbationwhere δ is a dimensionless real number much smaller than unity. Find the zeroth-order energy
Consider a symmetric rectangular double-well potential:Assuming that V0 is very high compared to the quantized energies of low-lying states, obtain an approximate expression for the energy splitting between the two lowest-lying states. for x > a+b; for a < x 0 for x|
Consider a particle in a two-dimensional potentialWrite the energy eigenfunctions for the ground state and the first excited state. We now add a time-independent perturbation of the formObtain the zeroth-order energy eigenfunctions and the first-order energy shifts for the ground state and the
Establish (5.1.54) for the one-dimensional harmonic oscillator given by (5.1.50) with an additional perturbation Show that all other matrix elements Vk0 vanish. 2 V = 1/εmw²x².
Evaluate the matrix elements (or expectation values) given below. If any vanishes, explain why it vanishes using simple symmetry (or other) arguments.[In (a) and (b), |nlm〉 stands for the energy eigenket of a nonrelativistic hydrogen atom with spin ignored.] (a) (n=2,1 1,m=0|x|n=2,1 (b) (n=2,1=1,
A slightly anisotropic three-dimensional harmonic oscillator has ωz ≈ ωx = ωy. A charged particle moves in the field of this oscillator and is at the same time exposed to a uniform magnetic field in the x-direction. Assuming that the Zeeman splitting is comparable to the splitting produced by
The Hamiltonian matrix for a two-state system can be written asClearly, the energy eigenfunctions for the unperturbed problems (λ = 0) are given by(a) Solve this problem exactly to find the energy eigenfunctions Ψ1 and Ψ2 and the energy eigenvalues E1 and E2.(b) Assuming thatsolve the same
A one-electron atom whose ground state is nondegenerate is placed in a uniform electric field in the z-direction. Obtain an approximate expression for the induced electric dipole moment of the ground state by considering the expectation value of ez with respect to the perturbed-state vector
Ap-orbital electron characterized by |n, l = l, m = ±1,0) (ignore spin) is subjected to a potential(a) Obtain the "correct" zeroth-order energy eigenstates that diagonalize the perturbation. You need not evaluate the energy shifts in detail, but show that the original threefold degeneracy is now
Consider a spinless particle in a two-dimensional infinite square well:(a) What are the energy eigenvalues for the three lowest states? Is there any degeneracy?(b) We now add a potentialTaking this as a weak perturbation, answer the following:(i) Is the energy shift due to the perturbation linear
Compute the Stark effect for the 2S1/2 and 2P1/2 levels of hydrogen for a field ε sufficiently weak that eεa0 is small compared to the fine structure, but take the Lamb shift δ (δ = 1,057 MHz) into account (that is, ignore lP3/2 in this calculation).Show that for the energy shifts are
A system that has three unperturbed states can be represented by the perturbed Hamiltonian matrixwhere E2 > E1· The quantities a and b are to be regarded as perturbations that are of the same order and are small compared with E2- E1. Use the second-order nondegenerate perturbation theory to
Consider a particle bound to a fixed center by a spherically symmetrical potential V(r).(a) Provefor all s-states, ground and excited.(b) Check this relation for the ground state of a three-dimensional isotropic oscillator, the hydrogen atom, and so on. (This relation has actually been found to be
(a) Suppose the Hamiltonian of a rigid rotator in a magnetic field perpendicular to the axis is of the formif terms quadratic in the field are neglected . Assuming B ≫ C, use perturbation theory to lowest nonvanishing order to get approximate energy eigenvalues.(b) Consider the matrix elementsof
Work out the Stark effect to lowest nonvanishing order for the n = 3 level of the hydrogen atom. Ignoring the spin-orbit force and relativistic correction (Lamb shift), obtain not only the energy shifts to lowest nonvanishing order but also the corresponding zeroth-order eigenket.
Work out the quadratic Zeeman effect for the ground-state hydrogen atom [(x|0) = (1/√πa03) e-r/a0] due to the usually neglected e2A2/2mec2- -term in the Hamiltonian taken to first order. Write the energy shift asand obtain an expression for diamagnetic susceptibility, X. The following definite
Suppose the electron had a very small intrinsic electric dipole moment analogous to the spin-magnetic moment (that is, μel proportional to σ). Treating the hypothetical -μel. E interaction as a small perturbation, discuss qualitatively how the energy levels of the Na atom (Z = 11) would be
Estimate the ground-state energy of a one-dimensional simple harmonic oscillator usingas a trial function with β to be varied. You may use (x|0) = e-Blx|
For the He wave function, usewith Zeff = 2 - 5/16, as obtained by the variational method. The measured value of the diamagnetic susceptibility is 1.88 x 10-6 cm3/mole.Using the Hamiltonian for an atomic electron in a magnetic field, determine, for a state of zero angular momentum, the energy,
Estimate the lowest eigenvalue (λ) of the differential equationusing the variational method withas a trial function. Numerical data that may be useful for this problem areThe exact value of the lowest eigenvalue can be shown to be 1 .019. d² y dx² +(2-x) = 0, 0 for|x|→ ∞
Consider a one-dimensional simple harmonic oscillator whose classical angular frequency is wo. For t 0 there is also a time-dependent potentialwhere F0 is constant in both space and time. Obtain an expression for the expectation value 〈x〉 as a function of time using time-dependent perturbation
A one-dimensional harmonic oscillator is in its ground state for t (a) Using time-dependent perturbation theory to first order, obtain the probability of finding the oscillator in its first excited state for t > 0. Show that the t → ∞ (τ finite) limit of your expression is independent of
The unperturbed Hamiltonian of a two-state system is represented byThere is, in addition, a time-dependent perturbation(a) At t = 0 the system is known to be in the first state, repre sented byUsing time-dependent perturbation theory and assuming that E01- E02 is not close to ±h̄ω, derive an
Consider a particle bound in a simple harmonic-oscillator potential. Initially (t < 0), it is in the ground state. At t = 0 a perturbation of the formis switched on. Using time-dependent perturbation theory, calculate the probability that after a sufficiently long time (t ≫ τ), the system
(a) Consider a pure ensemble of identically prepared spin 1/2 systems. Suppose the expectation values 〈Sx〉 and 〈Sz〉 and the sign of 〈Sy〉 are known. Show how we may determine the state vector. Why is it unnecessary to know the magnitude of 〈Sy〉?(b) Consider a mixed ensemble of spin
Show that the 3 x 3 matrices Gi(i = 1, 2, 3) whose elements are given bywhere j and k are the row and column indices, satisfy the angular-momentum commutation relations. What is the physical (or geometric) significance of the transformation matrix that connects Gi to the more usual 3 x 3
(a) Let J be angular momentum. (It may stand for orbital L, spin S, or Jtotal·) Using the fact that Jx, ly, lz(± ≡ Jx ± i Jy) satisfy the usual angular-momentum commutation relations, prove(b) Using (a) (or otherwise), derive the "famous" expression for the coefficient c_that appears in J² =
Consider a particle in one dimension moving under the influence of some timeindependent potential. The energy levels and the corresponding eigenfunctions for this problem are assumed to be known . We now subject the particle to a traveling pulse represented by a time-dependent potential,(a) Suppose
Consider a two-level system with E1 2. There is a time-dependent potential that connects the two levels as follows:At t = 0, it is known that only the lower level is populated-that is, c1(0) = 1, c2(0) = 0.(a) Findby exactly solving the coupled differential equation(b) Do the same problem using
(a) In the presence of a uniform and static magnetic field B along the z-axis, the Hamiltonian is given bySolve this problem to obtain the energy levels of all four states using degenerate time-independent perturbation theory (instead of diagonalizing the Hamiltonian matrix). Regard the first and
Show that the slow-tum-on of perturbation V → 7 Vent can generate a contribution from the second term in (5.7.36). VRH 2μ S₂ = -S, ħ - (5.6.36)
Consider an atom made up of an electron and a singly charged (Z = 1) triton (3H). Initially the system is in its ground state (n = 1, l = 0). Suppose the system undergoes beta decay, in which the nuclear charge suddenly increases by one unit (realistically by emitting an electron and an
Consider the spontaneous emission of a photon by an excited atom. The process is known to be an E1 transition. Suppose the magnetic quantum number of the atom decreases by one unit. What is the angular distribution of the emitted photon? Also discuss the polarization of the photon, with attention
Show that An (R) defined in (5.6.23) is a purely real quantity. An (R) i (n; t| [VR\n;t)], (5.6.23)
The ground state of a hydrogen atom (n = 1, l = 0) is subjected to a time-dependent potential as follows:Using time-dependent perturbation theory, obtain an expression for the transition rate at which the electron is emitted with momentum p. Show, in particular, how you may compute the angular
A particle of mass m constrained to move in one dimension is confined within 0 < x < L by an infinite-wall potentialObtain an expression for the density of states (that is, the number of states per unit energy interval) for high energies as a function of E. V = ∞ V = 0 for x < 0,x > L, for
Consider a potentialwhere V0 may be positive or negative. Using the method of partial waves, show that for the differential cross section is isotropic and that the total cross section is given bySuppose the energy is raised slightly. Show that the angular distribution can then be written asObtain
Estimate the radius of the 40Ca nucleus from the data in Figure 6.6 and compare to that expected from the empirical value ≈ 1.4A1/3 fm, where A is the nuclear mass number. Check the validity of using the first-order Born approximation for these data. dolde
A spinless particle is scattered by a weak Yukawa potentialwhere μ > 0 but V0 can be positive or negative. It was shown in the text that the first-order Born amplitude is given by(a) Using f(1)(θ) and assuming |δl| ≪ 1, obtain an expression for δ1 in terms of a Legendre function of the
Consider scattering by a repulsive δ-shell potential:(a) Set up an equation that determines the s-wave phase shift δ0 as a function of k(E = h̄2k2 /2m).(b) Assume now that γ is very large,Show that if tan kR is not close to zero, the s-wave phase shift resembles the hard-sphere result discussed
A spinless particle is scattered by a time-dependent potentialShow that if the potential is treated to first order in the transition amplitude, the energy of the scattered particle is increased or decreased by h̄ω. Obtain dσ/dΩ. Discuss qualitatively what happens if the higher-order terms are
Check explicitly the x - px uncertainty relation for the ground state of a particle confined inside a hard sphere: V = ∞ for r > a, V = 0 for r < a.
Prove[AB,C D] =- AC{D, B} + A{C, B}D - C{D, A}B + {C, A}DB.
Using the rules of bra-ket algebra, prove or evaluate the following:(a) tr(XY) = tr(Y X), where X and Y are operators.(b) (XY)† = Y† X†, where X and Y are operators.(c) exp[if(A)] =? in ket-bra form, where A is a Hermitian operator whose eigenvalues are known.(d) Σa (x) (x"), where a'(x) =
Using the orthonormality of |+〉 and | - 〉, provewhere [Si, Sj]=i&ijkh Sk. (Si, Sj): = 7/2 ħ² Sij,
A beam of spin 1/2 atoms goes through a series of Stem-Gerlach-type measurements as follows:(a) The first measurement accepts sz = h̄/2 atoms and rejects sz = -h̄2 atoms.(b) The second measurement accepts sn = h̄/2 atoms and rejects sn = -h̄/2 atoms, where sn is the eigenvalue of the operator S
Evaluate the x-p uncertainty product 〈(Δx)2 〉 〈(Δp)2〉 for a one-dimensional particle confined between two rigid walls,Do this for both the ground and excited states. 0 v = { % V for 0 < x
Let A and B be observables. Suppose the simultaneous eigenkets of A and B {|a′, b′〉} form a complete orthonormal set of base kets. Can we always conclude that [A, B] = 0?If your answer is yes, prove the assertion. If your answer is no, give a counterexample.
Estimate the rough order of magnitude of the length of time that an ice pick can be balanced on its point if the only limitation is that set by the Heisenberg uncertainty principle. Assume that the point is sharp and that the point and the surface on which it rests are hard. You may make

Modern Quantum Mechanics 2nd Edition J. J. Sakurai, Jim J. Napolitano - Solutions

Step by Step Answers