Consider a stochastic growth model with fixed labor supply and labor-augmenting technological shocks. Output \(Y_{t}\) is

for technology \(A_{t}\) and capital stock \(K_{t}\).
Capital is accumulated without adjustment costs:

where \(\delta\) is the capital depreciation rate and \(C_{t}\) is consumption. Consumption is chosen by a representative agent maximizing power utility with time discount factor \(\beta\), coefficient of relative risk aversion \(\gamma\), and elasticity of intertemporal substitution \(\psi=1 / \gamma\).

(a) Write an expression relating the one-period gross return on an investment in capital, \(1+R_{t+1}\), to the marginal product of capital in production and the depreciation rate.

(b) Consider the steady state (the nonstochastic balanced growth path) of the model in which technology is growing at a constant rate \(G\) :

(i) Use the equations for output and capital accumulation, and the first-order condition of the representative agent, to solve for the steady-state ratios \(A / K, Y / K\), and \(C / Y\) as functions of the \(\log\) technology growth rate \(g=\log (1+G)\), the \(\log\)

real return on capital \(r=\log (1+R)\), the capital share of output \(\alpha\), and the capital depreciation rate \(\delta\). You may assume \(g \approx G\) and \(r \approx R\). In this exercise, what is implicitly being assumed about the parameters \(\beta\) and \(\gamma\) ?
(ii) In a calibrated annual model with \(g=0.02, r=0.06, \alpha=0.333\), and \(\delta=0.10\), what values for \(Y / K\) and \(C / Y\) are implied?

(c) Now consider fluctuations around the steady state, writing lowercase letters for log deviations from steady state. We have

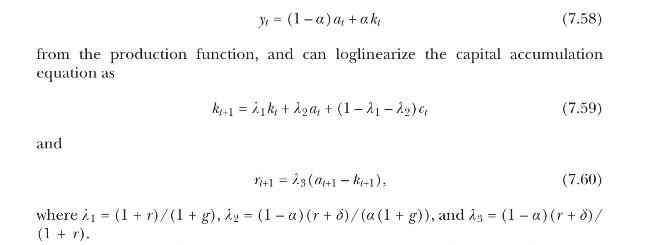
(i) In the calibrated example above, what are the values of \(\lambda_{1}, \lambda_{2}\), and \(\lambda_{3}\) ? Give an intuitive explanation for the magnitudes of \(1-\lambda_{1}-\lambda_{2}\) and \(\lambda_{3}\).
(ii) Show that the representative agent's first-order condition makes \(\mathrm{E}_{t} \Delta c_{t+1}\) proportional to \(\mathrm{E}_{t}\left(a_{t+1}-k_{t+1}ight)\). What is the coefficient of proportionality? Explain.

(d) We close the model by assuming an \(\mathrm{AR}(1)\) process for log technology deviations:

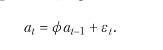
(i) We conjecture a solution of the form

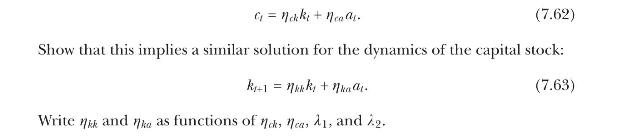
(ii) Conditional on the conjecture, derive a quadratic equation that \(\eta_{c k}\) must satisfy, and a linear equation for \(\eta_{c a}\) given \(\eta_{c k}\).

(e) The parameters have the following properties. In each case, explain the intuition:
(i) \(\eta_{c k}\) is increasing and \(\eta_{k k}\) is decreasing in the elasticity of intertemporal substitution \(\psi\). In the limit as \(\psi\) increases, \(\eta_{k k}\) approaches zero.
(ii) \(\eta_{c a}\) is increasing in persistence \(\phi\) for low values of \(\psi\), but decreasing in \(\phi\) for high values of \(\psi\).

(iii) When \(\phi=1, \eta_{c k}+\eta_{c a}=1\) and \(\eta_{k k}+\eta_{k a}=1\).
(iv) High values of \(\psi\) amplify the short-run response of output and dampen the longer-run response of output to a transitory technology shock.
(v) High values of \(\psi\) lead output to adjust more quickly to the new steady-state level of output when there is a permanent technology shock.

Transcribed Image Text:

Y = A *K,