Consider the function

for the concentration profile as a function of time. In practice, we need to truncate the sum with a finite number k terms,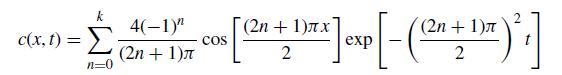

(a) Some functions are very difficult to represent as a Fourier series. The initial condition for this problem is one such function. Write a MATLAB program that automatically plots the value of c(x, 0) for different values of k. It is convenient to use the linspace function in MATLAB to generate values of x for this problem. You should choose values of k that illustrate the difficulty in making the plot. To help get you started with modular programming, your program should include a subfunction out=getc(x,t,k) that returns the value of c(x, t) for some position x and time t using k terms in the sum. Explain what happens to the behavior of the plot as a function of k. Also explain why the difference between the sum and the initial condition is different at x = 0 and x = 1.

(b) Now that we know how to plot the hardest solution, modify your program from part (a) to plot the concentration profile as a function of time. Pick a number of times for the plot that illustrate both the short-time and long-time behavior of the solution – in other words, it should be clear how the concentration profile is evolving as a function of time but the plot needs to be readable! Explain why your plot satisfies the boundary conditions and what happens at the steady state for the problem.

c(x, t) = n=0 4(-1)" (2n + 1) COS Dit]exp - (2 - + ] (2n + 1) 2 (2n + 1). 2