Consider the Lorenz equations with parameters = 10, b = 8/3, and r = 28. Employ initial conditions of x(0) = y(0) = z(0)

Consider the Lorenz equations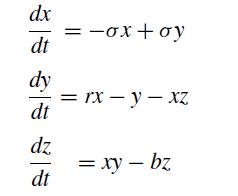

with parameters σ = 10, b = 8/3, and r = 28. Employ initial conditions of x(0) = y(0) = z(0) = 5 and integrate from t = 0 to 20. Use the Runge–Kutta fourth-order method for the integration with a time step of Δt = 0.031 25.

(a) For the above initial condition generate all three two-dimensional phase plots as well as the three-dimensional phase plot.

(b) Now consider a small perturbation in the initial condition for x (from 5 to 5.001). Compare the time trajectories of x for the two initial conditions. Is the system chaotic?

dx | | | dt dy dt dz dt = -ox+oy = rx - y - xz = xy - bz