Question: The system has a steady state at (x 1 = 1, x 2 = 1). You can analyze this steady state using linear stability analysis,

The system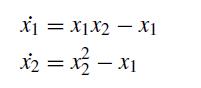 x = X1 X2 X1 x2 x = x - x

has a steady state at (x₁ = 1, x₂ = 1). You can analyze this steady state using linear stability analysis, or just consider the phase plane in Fig. 5.23. What can you say about the real and imaginary parts of the eigenvalues of the steady state Jacobian for this problem? You can provide a qualitative answer based on the phase plane or a numerical value based on linear stability analysis, whichever you prefer.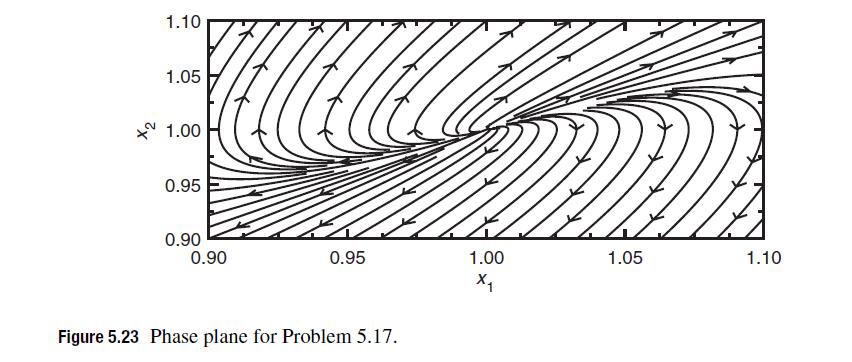 1.10 1.05 1.00 0.95 0.90 0.90 0.95 Figure 5.23 Phase plane for Problem 5.17. 1.00 X 1.05 1.10

x = X1 X2 X1 x2 x = x - x

Step by Step Solution

★★★★★

3.32 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Numerical Methods With Chemical Engineering Applications Questions!

Need to file tax return for this Tax Scenario Facts: Name SSN DOB Relationship Dana Taxpayer 305-44-0001 01/01/1990 Father George Taxpayer 305-44-0002 02/02/2018 Son Sara Taxpayer 305-44-0003...

In this problem, you will use your knowledge of the phase plane and stability to analyze a simple model of glycolysis. The glycolysis pathway that first convert glucose into fructose-6-phosphate...

-1.9(1) g (t) ait, where g is a differentiable function. The table above gives selected values for f, g, and g'. If h is the function given by h (a)=2-e+3, for which Let f be the function given by...

On January 1, 2025, Wildhorse Company purchased a machine costing $350000. The machine is in the MACRS 5-year recovery class for tax purposes and has an estimated $66000 salvage value at the end of...

Consider the Deer-Moose model whose vector field and trajectories are shown below. This model has four equilibrium points shown by the black dots. Explain in words what the basins of attraction of...

Consider the dynamical system (a) Use linear stability analysis to characterize the steady states in the interval x [3.5, 3.5] and y [3.5, 3.5]. You are not allowed to use the eigenvalue functions...

can you please answers all multiple choice answers please. Core Concepts of Accounting Information Systems, 13th Edition, by Simkin, Rose, and Norman Chapter 6 DEVELOPING AND IMPLEMENTING EFFECTIVE...

WebAssign Welcome, jeremy.guillory@grandcanyon (log out) Friday, November 11 2016 02:34 AM MST Home My Assignments Grades Communication Calendar My eBooks Notifications Help My Options MAT 274,...

please show all work from a to e. 3. The equations given above give very specific information about the system. Write an equation or set of equations, chosen only from the equations given above, that...

Discuss the how you would design a production system with respect to each of Askins/Standridges 9 manufacturing systems laws (p. 12-16) (pick a "production" domain (manufacturing, logistics, or...

References: Health Information Management Case Studies Second Edition AHIMA by Dianna M. Foley Health Information Management Technology an Applied Approah Sixth Edition AHIMA by Nanette Sayles and...

Assuming that the population is normally distributed, construct a 95% confidence interval estimate for the population mean for each of the following samples: Sample A: 1 1 1 1 8 8 8 8 Sample B: 1 2 3...

Wonder Company is experiencing financial difficulties and is negotiating a troubled debt restructuring with your creditors to alleviate your financial stress. Wonder has a P3,000,000 promissory note...

17. Which of the following are included in the calculation of net income but excluded in the calculation of NOPAT? a. Interest expense. b. Gains on investments. c. Losses on investments. d. All of...

Table 6.8 results from a clinical trial for the treatment of small-cell lung cancer. Patients were randomly assigned to two treatment groups. The sequential therapy administered the same combination...

The wind power output per unit area swept by the rotor is 2.4 kW/m 2 . Convert this quantity to the dimensions of hp/ft 2 .

A world-class runner can run half a mile in a time of 1 min and 45 s. What is the runners average speed in m/s?

One U.S. gallon is equivalent to 0.1337 ft 3 , 1 ft is equivalent to 0.3048 m, and 1000 L are equivalent to 1 m 3 . By using those definitions, determine the conversion factor between gallons and...

Springsteen Company manufactures guitars. The company uses a standard, job-order cost-accounting system in two production departments. In the Construction Department, the wooden guitars are built by...

Compute the number of equivalent units with respect to direct materials using the weighted-average method. Units Direct Materials Percent Complete Conversion Percent Complete Beginning work in...

When determining whether or not two firms are direct competitors, one can consider the level of resource congruity resource similarity