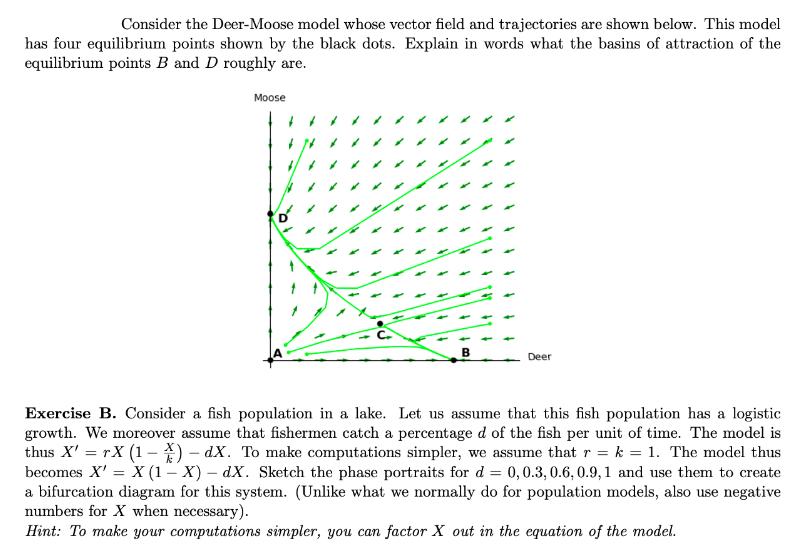
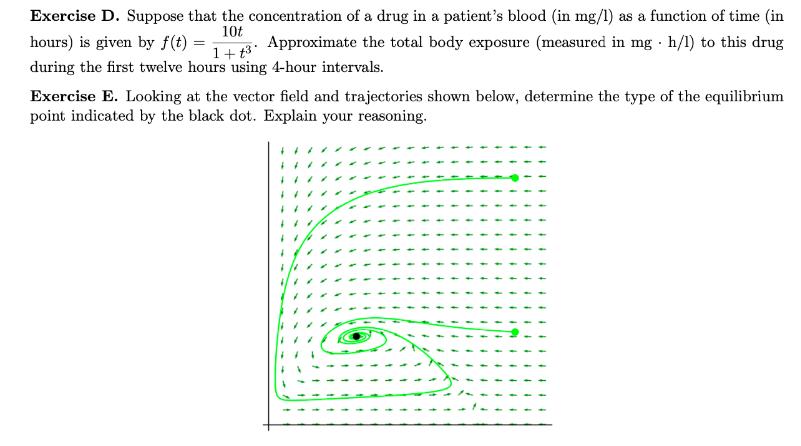
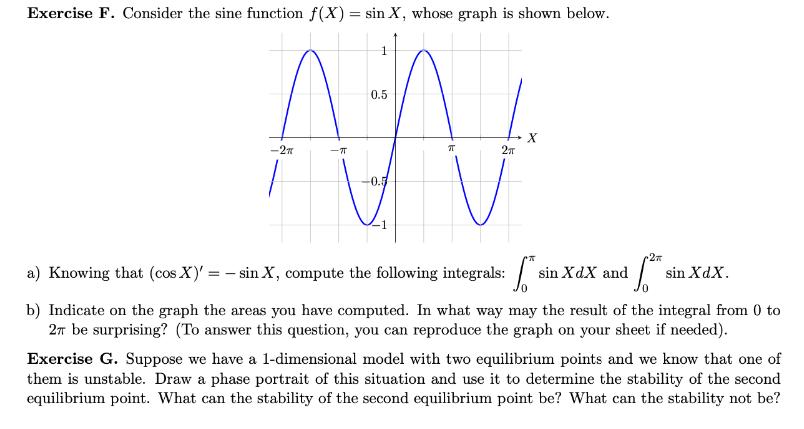
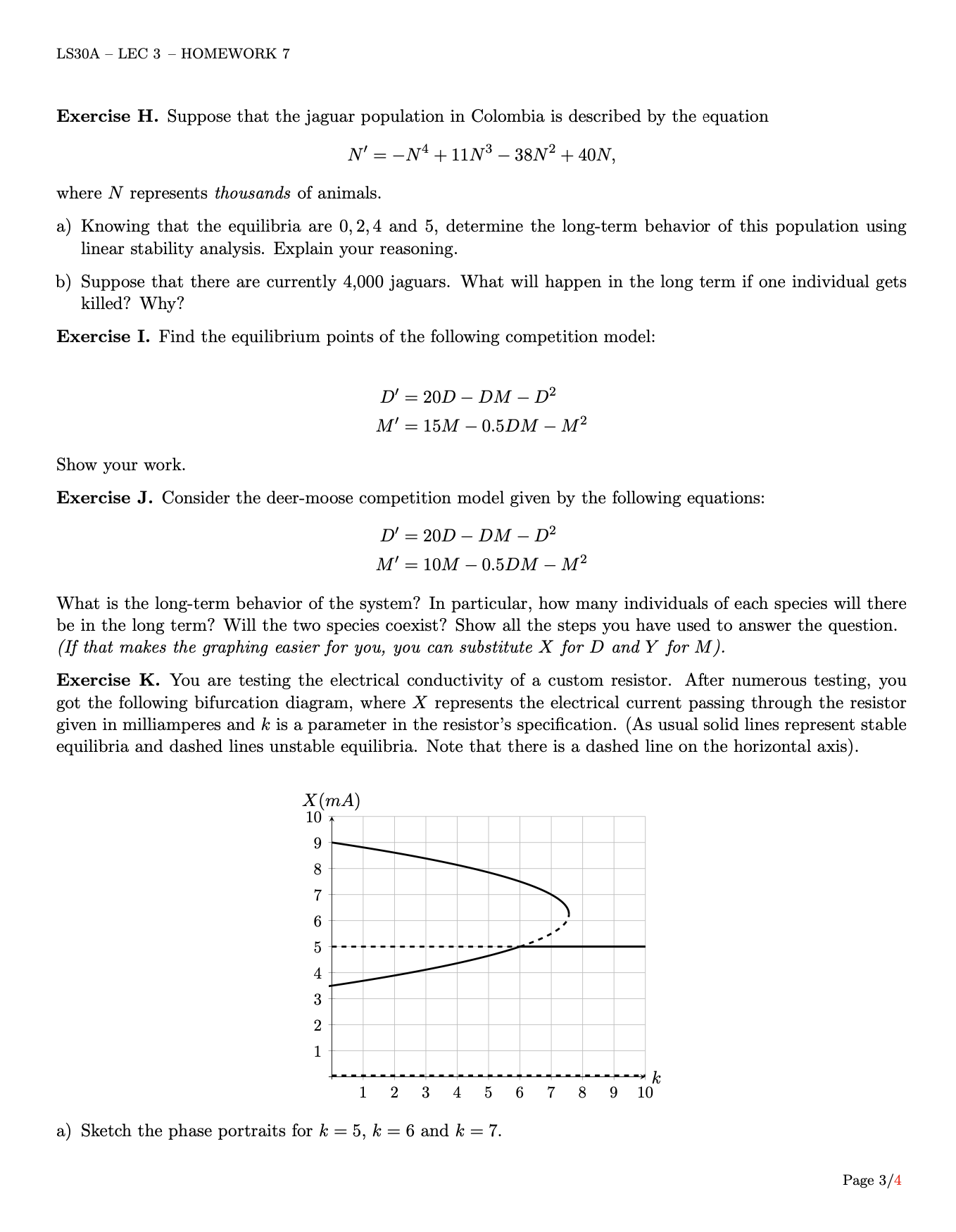
Consider the Deer-Moose model whose vector field and trajectories are shown below. This model has four equilibrium points shown by the black dots. Explain in words what the basins of attraction of the equilibrium points B and D roughly are. Moose B Deer Exercise B. Consider a fish population in a lake. Let us assume that this fish population has a logistic growth. We moreover assume that fishermen catch a percentage d of the fish per unit of time. The model is thus X' = rx (1) - dX. To make computations simpler, we assume that r = k = 1. The model thus becomes X' = X (1-X) - dX. Sketch the phase portraits for d = 0, 0.3, 0.6, 0.9, 1 and use them to create a bifurcation diagram for this system. (Unlike what we normally do for population models, also use negative numbers for X when necessary). Hint: To make your computations simpler, you can factor X out in the equation of the model. Exercise D. Suppose that the concentration of a drug in a patient's blood (in mg/l) as a function of time (in 10t hours) is given by f(t) = 1++3. Approximate the total body exposure (measured in mg h/l) to this drug during the first twelve hours using 4-hour intervals. Exercise E. Looking at the vector field and trajectories shown below, determine the type of the equilibrium point indicated by the black dot. Explain your reasoning. Exercise F. Consider the sine function f(x) = sin X, whose graph is shown below. 0.5 AN -2 X a) Knowing that (cos X)' = - sin X, compute the following integrals: sin XdX and 2 sin XdX. b) Indicate on the graph the areas you have computed. In what way may the result of the integral from 0 to 2 be surprising? (To answer this question, you can reproduce the graph on your sheet if needed). Exercise G. Suppose we have a 1-dimensional model with two equilibrium points and we know that one of them is unstable. Draw a phase portrait of this situation and use it to determine the stability of the second equilibrium point. What can the stability of the second equilibrium point be? What can the stability not be? LS30A LEC 3 - HOMEWORK 7 Exercise H. Suppose that the jaguar population in Colombia is described by the equation == N' N + 11N. -38N2 + 40N, where N represents thousands of animals. a) Knowing that the equilibria are 0, 2, 4 and 5, determine the long-term behavior of this population using linear stability analysis. Explain your reasoning. b) Suppose that there are currently 4,000 jaguars. What will happen in the long term if one individual gets killed? Why? Exercise I. Find the equilibrium points of the following competition model: D' =20D-DM - D M' = 15M 0.5DM M _ Show your work. Exercise J. Consider the deer-moose competition model given by the following equations: D'20DDM - D M' = 10M0.5DM - M What is the long-term behavior of the system? In particular, how many individuals of each species will there be in the long term? Will the two species coexist? Show all the steps you have used to answer the question. (If that makes the graphing easier for you, you can substitute X for D and Y for M). Exercise K. You are testing the electrical conductivity of a custom resistor. After numerous testing, you got the following bifurcation diagram, where X represents the electrical current passing through the resistor given in milliamperes and k is a parameter in the resistor's specification. (As usual solid lines represent stable equilibria and dashed lines unstable equilibria. Note that there is a dashed line on the horizontal axis). X(mA) 10+ 9 8 7 6 07 05 5 4 3 21 k 1 2 3 4 5 6 7 8 9 10 a) Sketch the phase portraits for k = 5, k = 6 and k = 7. Page 3/4 b) Suppose that the current value of k is k = 7, and X has stabilized at X = 5 what will happen to X if k is lowered to k = 2? c) The main purpose of a resistor is to control the flow of electricity in a circuit. The electrical system is currently sitting at a stable current of X = 4, but for our purpose, we need it to reach a stable current of X = 8.5. Suppose you have the ability to manipulate k at will, and temporarily increase the current in the circuit by 0.5. Explain how we can bring X to 8.5 or why it is not possible.