This problem takes a closer look at flow inside a square duct. Read this entire problem statement first. You should try to construct your programs in parts (a) and (b) in a way that makes it easier for you to solve part (c).

(a) For flow inside a square duct the dimensionless velocity profile is given by the infinite series solution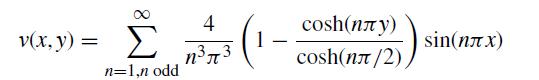

where x ∈ [0, 1] and y ∈ [−1/2, 1/2]. Make a MATLAB program that plots this solution using mesh for 100 equally spaced nodes in x and y. You should use enough points in the sum so that the result is not changing much as you add more terms.

(b) The flow in a square duct is the solution to the Poisson equation,

subject to v = 0 on the boundaries. Write a MATLAB program that solves this equation using centered finite differences with 100 nodes per side using a sparse solver. Your program should automatically plot the solution.

(c) Let’s now figure out the accuracy of the numerical solution. Write a MATLAB program, using the programs that you already wrote, that computes

where v is the infinite series results (with k terms sufficient to provide accuracy) and ˜v is the numerical solution (with n nodes on each side). You can think of this as an error in the solution, assuming that you use enough terms in the infinite series. Your program should automatically make a log–log plot of the error versus the number of nodes for a fixed number of terms in the infinite sum.

v(x, y) = n=1,n odd 4 3 1 - cosh(nay) cosh(/2) sin(.)