Let the random variable X be defined as the number of coin tosses needed to obtain the first heads, given that successive tosses are independent, the probability that each toss is heads is given by p, and the probability that each coin is tails is given by q 1 p. Then X follows a geometric random variable, where

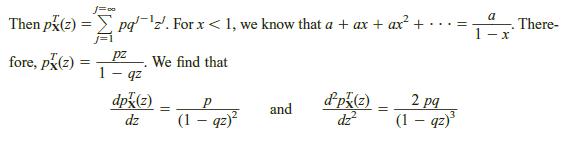
Letting z =1 (Equation (23)) tells us that

Suppose X1, X2, . . . , Xn are independent random variables. Let S = X1 + X2 +.........
+ Xn. Then it is easy to prove (see Problem 2) that

P(X = j) = pq (j = 1, 2,...,n).