Imagine that we have a large photographic transparency on which there is a picture of a student made up of a regular array of small circular dots, all of the same size, but each with its own density, so that it passes a spot of light with a particular field amplitude. Considering the transparency to be illuminated by a plane wave, discuss the idea of representing the electric-field amplitude just beyond it as the product (on average) of a regular two-dimensional array of top-hat functions (Fig. 11.4) and the continuous two-dimensional picture function: the former like a dull bed of nails, the latter an ordinary photograph. Applying the frequency convolution theorem, what does the distribution of light look like on the transform plane? How might it be filtered to produce a continuous output image?

Fig. 11.4

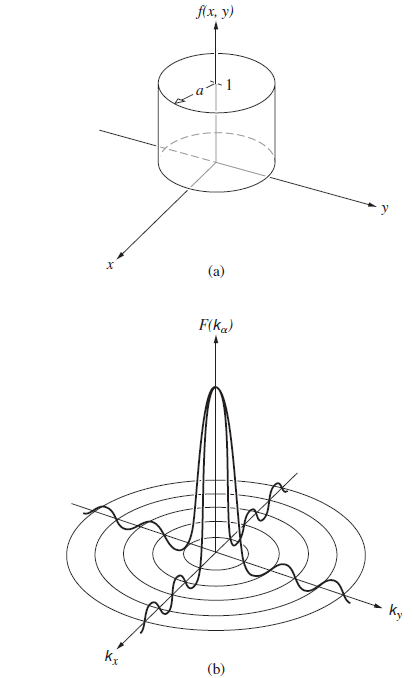
, ) (a) F(ka) Ky kg (b)