1. Let : R m R k and g : R n R m be two maps. Let h : R n

1. Let ƒ : R^m → R^k and g : Rⁿ → R^m be two maps. Let h : Rⁿ→ R^k be the composite map h = ƒ ο g, with values h(x) = ƒ(g(x)) for x ∈ Rⁿ. Show that the derivatives of h can be expressed via a matrix-matrix product, as J_h(x) = J_ƒ (g(x)) · J_g(x), where J^h(x) is the Jacobian matrix of h at x, i.e., the matrix whose (i, j) element is .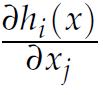

2. Let g be an affine map of the form g(x) = Ax + b, for A ∈ R^m,n, b ∈ R^m. Show that the Jacobian of h(x) = ƒ(g(x)) is

3. Let g be an affine map as in the previous point, let ƒ: Rⁿ → R (a scalar-valued function), and let h(x) = ƒ(g(x)). Show that

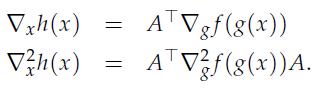
h;(x) ;