A second-degree polynomial with values p(x) = y₀ + y₁x + y2x² is non-negative everywhere if and only if

which in turn can be written as an LMI in y = (y₀, y₁, y₂):

In this exercise, you show a more general result, which applies to any polynomial of even degree 2k (polynomials of odd degree can’t be non-negative everywhere). To simplify, we only examine the case k = 2, that is, fourth-degree polynomials; the method employed here can be generalized to k > 2.

1. Show that a fourth-degree polynomial p is non-negative everywhere if and only if it is a sum of squares, that is, it can be written as

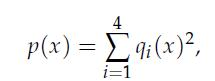
where q_i’s are polynomials of degree at most two.

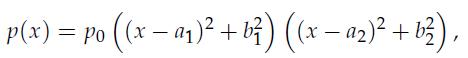
for some appropriate real numbers a_i, b_i, i = 1, 2, and some p₀ ≥ 0.

2. Using the previous part, show that if a fourth-degree polynomial is a sum of squares, then it can be written as.

for some positive-semidefinite matrix Q.
3. Show the converse: if a positive semi-definite matrix Q satisfies condition (11.25) for every x, then p is a sum of squares. 

4. Show that a fourth-degree polynomial   is non-negative everywhere if and only if there exist a 5 x 5 matrix Q such that

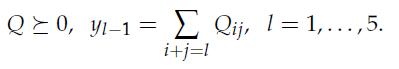
[F][/] 0 Yo Y1/2 X Y1/2 Y2 Vx: X 1 1