Question: Consider the unconstrained optimization problem where are given. The goal of this exercise is to determine the optimal value p and the set of optimal
Consider the unconstrained optimization problem
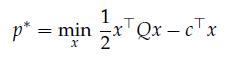
where![]() are given. The goal of this exercise is to determine the optimal value p and the set of optimal solutions,
are given. The goal of this exercise is to determine the optimal value p and the set of optimal solutions, ![]() ,in terms of c and the eigenvalues and eigenvectors of the (symmetric) matrix Q.
,in terms of c and the eigenvalues and eigenvectors of the (symmetric) matrix Q.
1. Assume that ![]() Show that the optimal set is a singleton, and that p is finite. Determine both in terms of Q, c.
Show that the optimal set is a singleton, and that p is finite. Determine both in terms of Q, c.
2.

3. Now we do not assume that Q is diagonal anymore. Under what conditions (on Q, c)) is the optimal value finite? Make sure to express your result in terms of Q and c, as explicitly as possible.
Now we do not assume that Q is diagonal anymore. Under what
conditions (on Q, c) is the optimal value finite? Make sure to express
your result in terms of Q and c, as explicitly as possible.
4. Assuming that the optimal value is finite, determine the optimal value and optimal set. Be as specific as you can, and express your results in terms of the pseudo-inverse5 of Q.
p* T 1 1/2 x Qx - c x = min x
Step by Step Solution
3.42 Rating (155 Votes )
There are 3 Steps involved in it
1 When it admits a Cholesky decomposition with R uppertriangular and invertible We can define the ne... View full answer

Get step-by-step solutions from verified subject matter experts


