Question: Let A R n,n and let be the characteristic polynomial of A. 1. Assume A is diagonalizable. Prove that A annihilates its own characteristic

Let A ∈ R^n,nand let

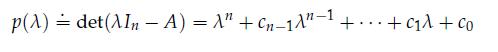
p(A) = det(^In A) = A + Cn-1^"-1 +...+c + co

be the characteristic polynomial of A.

1. Assume A is diagonalizable. Prove that A annihilates its own characteristic polynomial, that is

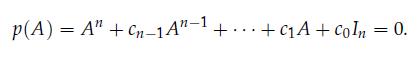
2. Prove that p(A) = 0 holds in general, i.e., also for non-diagonalizable square matrices.

p(A) = det(^In A) = A + Cn-1^"-1 +...+c + co

Step by Step Solution

★★★★★

3.39 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To address both parts of the question well start by clarifying some notations and concepts Given a matrix A Rnn its characteristic polynomial is defin... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Optimization Models Questions!

The Cayley-Hamilton Theorem: Let pA () = det(A - I) be the characteristic polynomial of A. (a) Prove that if D is a diagonal matrix, then pD(D) = O. (b) Prove that if A is complete, then pA(A) = O....

Let A be any n ( n real matrix. (a) Prove that the coefficient of (n-1 in the characteristic polynomial of A is given by - Tr(A). (b) Prove that Tr(A) is the sum of the eigenvalues of A. (c) Prove...

Let p() = (-1 )n(n - n-1n-1 -....- 1 - o) he a polynomial of degree n I (a) Show that if i, is a root of p() = 0 then i is an elgenvalue of C with eigenvector x = (in-1,, in-2...... i,1)T , (b) Use...

4. Let A be a diagonalizable matrix, with characteristic polynomial det(AI - A) = (1 - c)" for some constant cE R. Prove that A = cl, where I is the n x n identity matrix

(1) Prove or disprove : there exist a basis po, pi, p2, pa E PY(R) ( Py(R) is the set of all polynomial over real number with highest possible degree = 3 ) such that none of poly- nomials po. P1, p2,...

9. Let T be a linear operator on a nite-dimensional vector space V, and suppose there exists an ordered basis if for V such that [T] 5 is an upper triangular matrix. (a) Prove that the characteristic...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

,, kindly solve Consider the Linear Regression Model 1. For any X = x, let Y = x8 + U, where B E R*. 2. X is exogenous. 3. The probability model is { f (u; ) is a distribution on R : E, [U] = 0, Var,...

HEY CAN YOU HELP ME SOLVE THE FOLLOWING QUESTIONS: 63, 65, 73, 81, 82, 83 5.3 Diagonalization of Matrices 323 57. [_7 3]: ([:] . ): 43 74. Find a 2 x 2 matrix having eigenvalues 7 and -4, with 58. 2...

Please Answer True Or False. No Need For Explanation. Thank You Very Much!!! 3. Let A and B be two square matrices over a field F. Assume that A and B have the same characteristic polynomial. Assume...

The hotel you own is being sued. You better find a lawyer to represent you fast. So search online and find one. Here's the hard part: They can't be personal injury lawyers who represent plaintiffs....

Suppose that the firm's demand curve indicates that at a price of $10 per unit, customers will demand 2 million units of its product. Suppose that management decides to pick both price and output;...

1. The circular fl ow model is a simplifi ed version of our economy. Describe how this model works.

Choose afederal,state,andlocalpublicorganization.Thiscouldbealibrary, elected representative,agency,orthelike. a. What socialmediapresencedoeseachorganizationhave? b. For...

Answer Problem 3.95 if the first birth was a live birth? Demography A study based on data collected from the Medical Birth Registry of Norway looked at fertility rates according to survival outcomes...

If the clinical diagnosis is considered a screening test for Alzheimers disease, then what is the sensitivity of this test? Mental Health The 4 allele of the gene encoding apolipoprotein E (APOE) is...

What is the specificity of this test? Mental Health The 4 allele of the gene encoding apolipoprotein E (APOE) is strongly associated with Alzheimers disease, but its value in making the diagnosis...

H.J. Heinz Company uses standards to control its materials costs. Assume that a batch of ketchup (7,650 pounds) has the following standards: Ingredient Standard Quantity Standard Price Whole tomatoes...

Just Need Yellow boxes filled out: March 15, 1 yellow box under Cost of Goods sold= March 15, 2 yellow boxes under Inventory Balance = July 30, 2 yellow boxes under Inventory Balance = October 5, 3...

Cane Company manufactures two products called Alpha and Beta that sell for $185 and $150, respectively. Each product uses only one type of raw material that costs $8 per pound. The company has the...