The returns on n = 4 assets are described by a Gaussian (Normal) random vector r ∈ Rⁿ, having the following expected value ˆr and covariance matrix ∑:

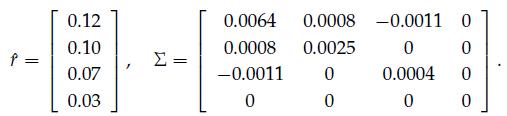
The last (fourth) asset corresponds to a risk-free investment. An investor wants to design a portfolio mix with weights x ∈ Rⁿ (each weight x_i is nonnegative, and the sum of the weights is one) so to obtain the best possible expected return r̂ ^T x, while guaranteeing that: 

(i) No single asset weights more than 40%; 

(ii) The risk-free assets should not weight more than 20%; 

(iii) No asset should weight less than 5%; 

(iv) The probability of experiencing a return lower than q = –3% should be no larger than ϵ = 10^–4. What is the maximal achievable expected return, under the above constraints?

P = 0.12 0.10 0.07 0.03 = 0.0064 0.0008 0.0008 0.0025 -0.0011 0 0 0 0.0011 0 0.0004 0 0 0 0 0