We are given a graph as a set of vertices in V = f{, . . . , n}, with an edge joining any pair of vertices in a set We assume that the graph is undirected (without arrows), meaning that (i, j) ∈ E implies (j, i) ∈ E. As in Section 4.1, we define the Laplacian matrix by

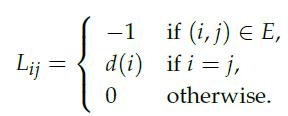
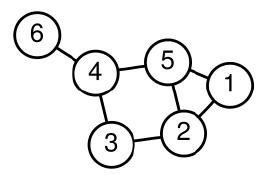
Here, d(i) is the number of edges adjacent to vertex i. For example, d(4) = 3 and d(6) = 1 for the graph in Figure 4.4.
1. Form the Laplacian for the graph shown in Figure 4.4.
2. Turning to a generic graph, show that the Laplacian L is symmetric.
3. Show that L is positive-semidefinite, proving the following identity, valid for any u ∈ Rⁿ: Find the valuesfor two unit vectors ek, el such that (k, l) ∈ E.

4. Show that 0 is always an eigenvalue of L, and exhibit an eigenvector.

5. The graph is said to be connected if there is a path joining any pair of vertices. Show that if the graph is connected, then the zero eigenvalue is simple, that is, the dimension of the null space of L is 1.Prove that if u^TLu = 0, then u_i = u_j for every pair (i, j) ∈ E.

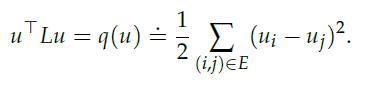
EC V X V. x