A small-angle approximation was used to derive Eq. 15. 31, \(\tau=-(m \ell g) \vartheta .(a)\) What constitutes small in this context? In other words, how large can \(\vartheta\) be before it can no longer be called small? (b) As a quantitative benchmark, how large does \(\vartheta\) have to be before \((m \ell g) \vartheta\) deviates by more than \(1 \%\) from the true value of \(\tau\) ?

Data from Eq. 15. 31

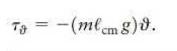
-(mlcmg)d.