For a light ray that crosses the interface between medium 1 having index of refraction \(n_{1}\) and medium 2 having index of refraction \(n_{2}\), what relationship between \(\theta_{1}\) and \(\theta_{2}\) follows from Fermat's principle (page 1155)?

Data from page 1155

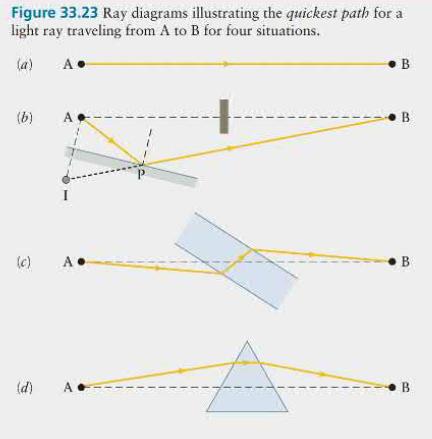
Figure 33.23 shows four ways in which a light ray can travel between two locations A and B: directly, reflected from a mirror, refracted through a glass slab, and refracted through a prism.* You could say that in each case the ray reaches B because it is aimed properly from A. However, an entirely different way of looking at the path followed by the light was suggested by the French mathematician Pierre de Fermat (1601-1665) in a formulation today known as Fermat's principle: The path taken by a light ray between two loca- tions is the path for which the time interval needed to travel between those locations is a minimum.