Show that an arbitrary n × n unitary matrix has n²real parameters, and hence that

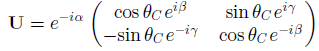
is the most general form of a 2 × 2 unitary matrix. The most general form of (d, s) mixing is

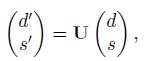
where U is an arbitrary 2 × 2 unitary matrix, U^U = 1. Show that this can be reduced to the form (9.39) by adjusting the arbitrary phases of the quark states s, s' and d.

Transcribed Image Text:

sin Oceiy cos Oce-iß U = e-ia cos Oc eB -sin Oce-iy