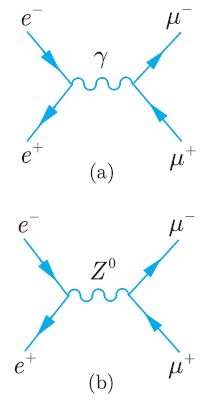
The centre-of-mass differential cross-section for the reaction e + e μ + μ due to the one-photon exchange diagram in Figure 10.2(a) is given in

The centre-of-mass differential cross-section for the reaction e⁺e^ˆ’†’ μ⁺μ^ˆ’due to the one-photon exchange diagram in Figure 10.2(a) is given in Equation (7.15),

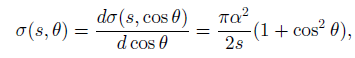
where s = E²_CM, θ is the scattering angle and we have, as usual, neglected the lepton masses compared to E_CM. When Z⁰ exchange is taken into account, this expression is modified to become

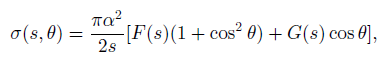
With

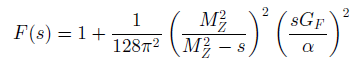
and

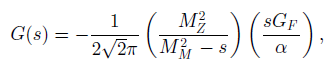
where we have assumed M²_Z ˆ’ s >> Γ_Z and sin² θ_W = 1/4. The terms in σ(s, θ) proportional to α², G²_F and αG_F arise from photon exchange, Z⁰ exchange and the interference between the two diagrams of Figure 10.2, respectively. Use these formulas to obtain expressions for the total cross-section σ_tot(s) and the forward€“ backward asymmetry parameter

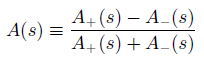
in terms of F(s) and G(s), where

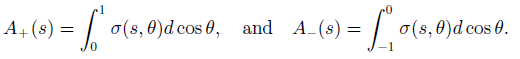
Hence evaluate the magnitude of A(s) and the percentage correction to the QED total cross-section σ_γ = 4πα²/3s at E_CM = M_z /3 ‰ˆ 30 GeV generated by the Z⁰ exchange contribution.

Figure 10.2

do (s, cos 0) (1+cos 0), TQ? ( 6,) - d cos 0 2s (s, ) - ? [F (s) (1 + cos ) + G(s) cos , 2s