A continuous adiabatic flash tank is to be used to separate a liquid mixture of two substances (A and B). The feed enters at temperature T_­ and a high pressure and flashes to a low pressure, P, whereupon its temperature drops to T. For an assumed basis of 1 mol/s of feed, let

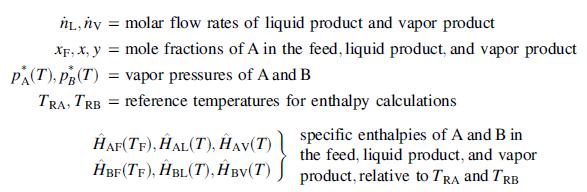
(a) Derive the following relations from Raoult’s lawand material and energy balances on the flash tank:

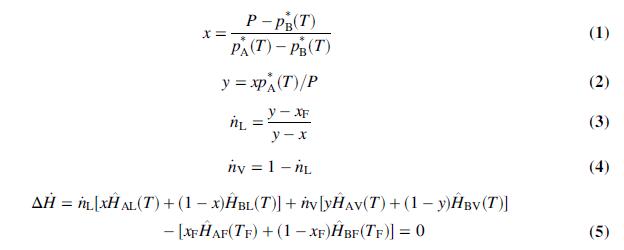
(b) Write a spreadsheet program to perform flash calculations for a feed mixture of n-pentane and n-hexane. When calculating enthalpies of these species, the following heat capacity formulas should be used for liquid and vapor, respectively:

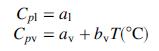
The spreadsheet should have the following form. Some values are given, others should be looked up in data tables, and the remainder should be calculated from Equations 1 to 5 and appropriate formulas for specific enthalpies.

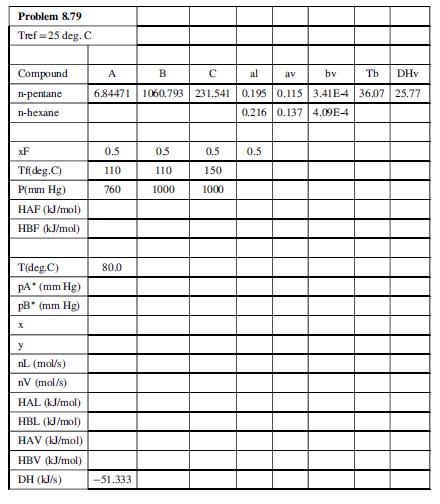
In this table, A, B, and C are Antoine equation constants, al, av, and bv are the coefficients of the given heat capacity formulas; Tb(°C) and DHv(kJ/mol) (ΔĤ_v) are the normal boiling point and heat of vaporization, xF(mol pentane/mol) is the mole fraction of pentane in the feed, Tf(°C) is the feed temperature, P(mm Hg) is the system pressure, HAF (Ĥ_AF) and HBF (Ĥ_BF) are the specific enthalpies of pentane and hexane in the feed stream, pA* is the vapor pressure of n-pentane (to be determined using the Antoine equation), x and n̂_L (x and n̂L) are the mole fraction of pentane in the liquid product stream and the molar flow rate of that stream, respectively, y and n_V are the corresponding properties of the vapor product stream, HAL is the specific enthalpy of pentane in the liquid product stream, and DH (ΔḢ ) is the expression given in Equation 5 for the change in total enthalpy from inlet to outlet.

Enter the appropriate constants and formulas for A, B, C, al, av, bv, Tb, and DHv for n-pentane and n-hexane, an initial guess for T in Column 2 (= 80.0), and the appropriate formulas for the rest of the variables in Column 2. Then vary the value of T until the value of ΔḢ is suitably close to zero, using the Goal Seek tool. The value of ΔḢ (-51.33 kJ/s) corresponding to the initial guess of 80°C is shown in the second column of the table. Your spreadsheet should generate the same value.

After completing the calculations in the second column, copy the formulas into the third and fourth columns and perform the calculations for these two sets of input parameter values. State how increasing the system pressure and feed temperature affect the fraction of the feed vaporized (nV) and the final system temperature (T), and briefly explain why your results make sense.

Transcribed Image Text:

İL, iv = molar flow rates of liquid product and vapor product XF, X, y = mole fractions of A in the feed, liquid product, and vapor product PA(T), PR(T) = vapor pressures of A and B TRA, TRB = reference temperatures for enthalpy calculations specific enthalpies of A and B in the feed, liquid product, and vapor product, relative to TRA and TRB HAF(TF), HAL(T), ĤAV(T) HBF(TF), HBL(T), HBV(T)