Consider the entangled wave function for two photons,

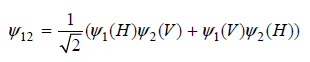
Assume that the polarization operator Pˆ_i has the properties Pˆψ_i i (H) = ˆ’ψ _i (H) and Pˆ_iψ i (V ) = + ψ _i (V ), where i = 1 or i = 2. H and V designate horizontal and vertical polarization, respectively.

a. Show that ψ₁₂ is not an eigenfunction of Pˆ₁ or Pˆ₂.

b. Show that each of the two terms in ψ₁₂ is an eigenfunction of the polarization operator Pˆ₁.

c. What is the average value of the polarization P₁ that you will measure on identically prepared systems?

Transcribed Image Text:

-(,(H)w,(V) + ¥¼(V)w2(H)) V12 =