Consider the general first-order linear equation y'(t) + a(t)y(t) = f(t). This equation can be solved, in principle, by defining the integrating factor p(t) = exp(∫ a(t) dt). Here is how the integrating factor works. Multiply both sides of the equation by p (which is always positive) and show that the left side becomes an exact derivative. Therefore, the equation becomes

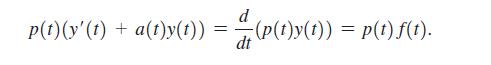
Now integrate both sides of the equation with respect to t to obtain the solution. Use this method to solve the following initial value problems. Begin by computing the required integrating factor.

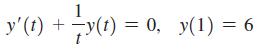
p(t) (y'(t) + a(t)y(t)) = d (P (p(t)y(t)) = p(t) f(t). dt