Let u (u 1 , u 2 , u 3 ), v (v 1 , v 2 , v 3 ), and w (w 1 , w 2 , w 3 ) Let c be a scalar Prove the following vector properties a Show that (u v) (u v) u 2u v v b Show that (u v) (u v) u v if u is perpendicular to v c Show that (u v) (u v) u v

Question: Let u = (u 1 , u 2 , u 3 ), v = (v 1 , v 2 , v 3 ), and w

Let u = (u₁, u₂, u₃), v = (v₁, v₂, v₃), and w = (w₁, w₂, w₃). Let c be a scalar. Prove the following vector properties.

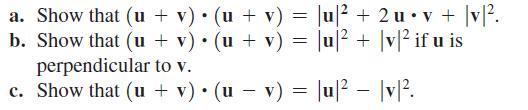
$. a. Show that (u + v) (u + v) = \u$

. a. Show that (u + v) (u + v) = \u + 2u.v + |v|. b. Show that (u + v) (u + v) = ]u[ + |v| if u is perpendicular to v. c. Show that (u + v) (u v) = ]u[ |v|. -

Step by Step Solution

★★★★★

3.45 Rating (152 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

ANSWER To prove the given vector properties well use the properties of dot product and vector magnit... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus 1st Questions!

Company B had estimated 100000 direct labor hours 400000 manufacturing overhead and 25000 machine hours The actual were 100700 direct labor hours 26600 machine hours and 475000 manufacturing overhead...

Let U1 and U2 be independent random variables. Suppose that U1 is X2 with v1 degrees of freedom while U = U1 + U2 is chi-square with v degrees of freedom, where v > v1. Then prove that U2 is...

Let A be a 3 ( 4 matrix, let v1 and v2 be vectors in, and let w = v1 + v2. Suppose v1 = Au1 and v2 = Au2 for some vectors u1 and u2 in. What fact allows you to conclude that the system Ax = w is...

Please tutors guide me on this question Consider the algebraic transpose IT : Yf - Xy associated with the linear operator L : X - Y, where X and Y are linear vector spaces and Xy and Yf are their...

Chapter 1 Euclidean spaces 12. Let u = (1, - 1, 0, 2), v = (- 2, - 1, 1, - 4), and w = (3, 2, - 1, 0). a. Find a vector a E R* such that 21 - 3v - d = W. b. Find a vector a 5 [2u - 3v + a] = 2w+...

Let u = (1, 1, 0, 2), v = = (3, 2, 1, 0). (-2, 1, 1, 4), and w Compute u v, u w, and w v.

Let u = (1, 1, 0, 2), v = (-2, 1, 1, 4), and w = (3, 2, 1, 0). a. Find a vector a ER4 such that 2 u 3 v - 37 a = w. b. Find a vector a 12 3 + ] = 2 w + d -2. | 2

f = function, b = accumulator, t = tree Please code in OCaml language. I have done this function already, but for some reason I'm getting errors, or it's not building my tree correctly, so I need...

title: "Homework 5" output: pdf_document --\\begin{center} \\textit{Due May 13, 2016 before 11:59 PM via upload to CCLE} \\end{center} \\section{Swirl Package} \\textbf{Problem 1.} - Start swirl and...

Please code in OCaml language. Given the type tree and the provided function tree_fold (fold_tree), please code the function compose using tree_fold (fold_tree) method with the description provided...

How would you assess the economic value of two SUVs?

The centralized employee travel department of Ohno Company has expenses of $210,000. The department has made serviced a total of 3,000 travel reservations for the period. The north-east division has...

( a ) State the three conditions that must be satisfied for a function f ( x ) to be continuous at a point m . ( b ) At what point ( s ) is this function f ( x ) = 3 x - 2 discontinuous, and what...

13.5 Explain the role of biopsychosocial factors in womens higher vulnerability to depression. (APA 1.3, 2.1, 2.5)

For the following exercises, determine the value of the annuity for the indicated monthly deposit amount, the number of deposits, and the interest rate. Write an explicit formula for a k such that...

For the following exercises, use the information provided to graph the first five terms of the geometric sequence. Use recursive formulas to give two examples of geometric sequences whose 3 rd terms...

For the following exercises, find the distinct number of arrangements. Just-For-Kicks Sneaker Company offers an online customizing service. How many ways are there to design a custom pair of...

The procedure used by the IRS to match the information recorded on a return with corresponding data received from third parties is commonly referred to as the: a. Information Document Reconciliation...

The Lark Company purchases a warehouse on December 31, 2014 for $130,000 (which includes all capitalizable costs). They put the warehouse into service on January 1, 2015, assigning it a useful life...

The following information is available for Sunland Company for the year ended December 31, 2017. Beginning cash balance $ 46,620 Accounts payable decrease 3,833 Depreciation expense 167,832 Accounts...