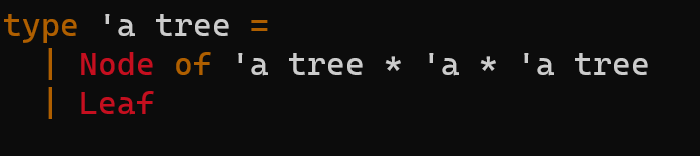
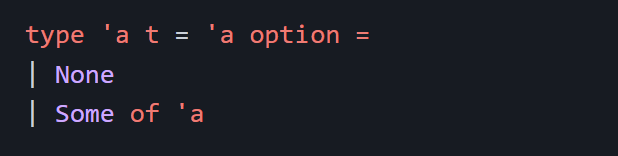
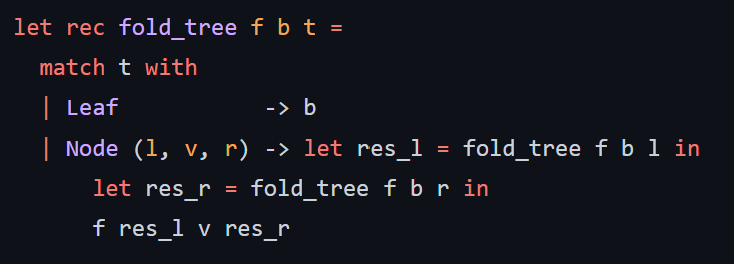
f = function, b = accumulator, t = tree

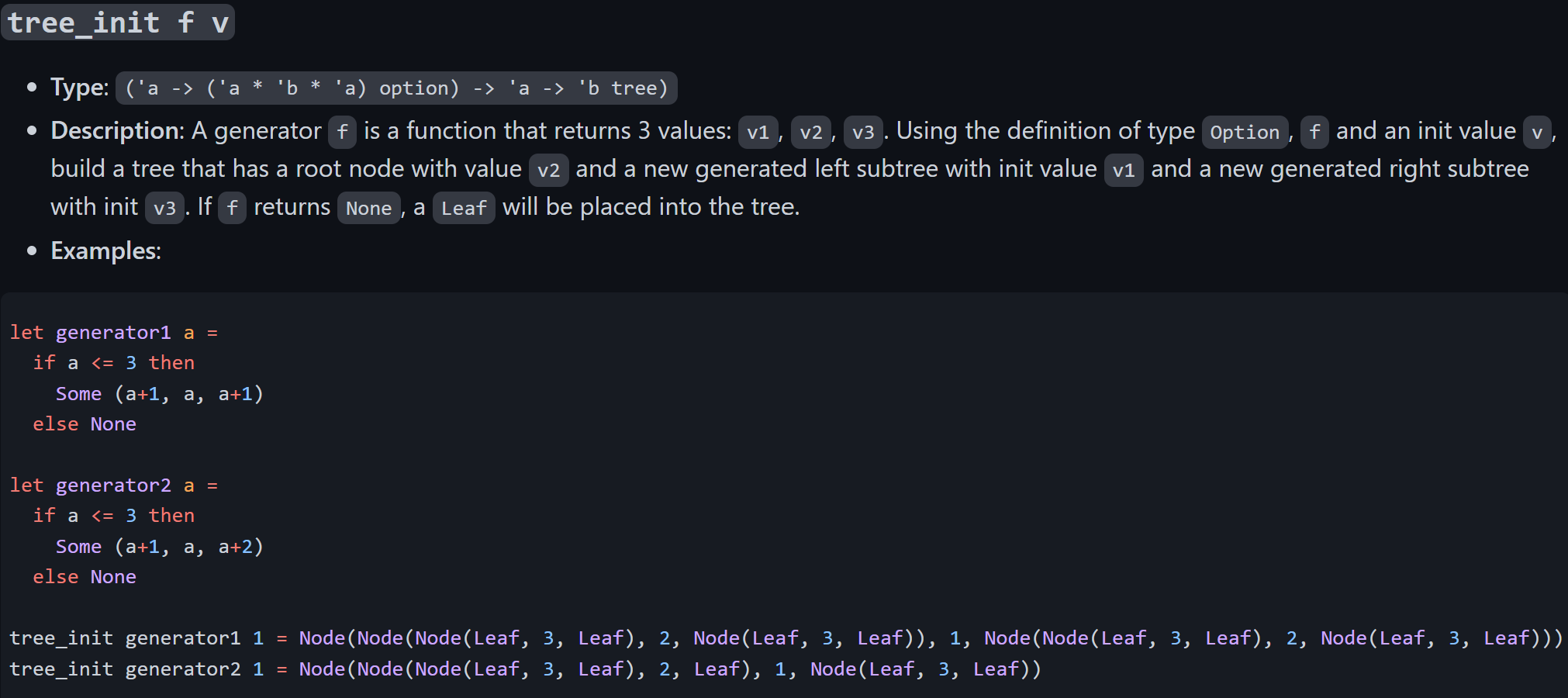
Please code in OCaml language. I have done this function already, but for some reason I'm getting errors, or it's not building my tree correctly, so I need assistance with this program.

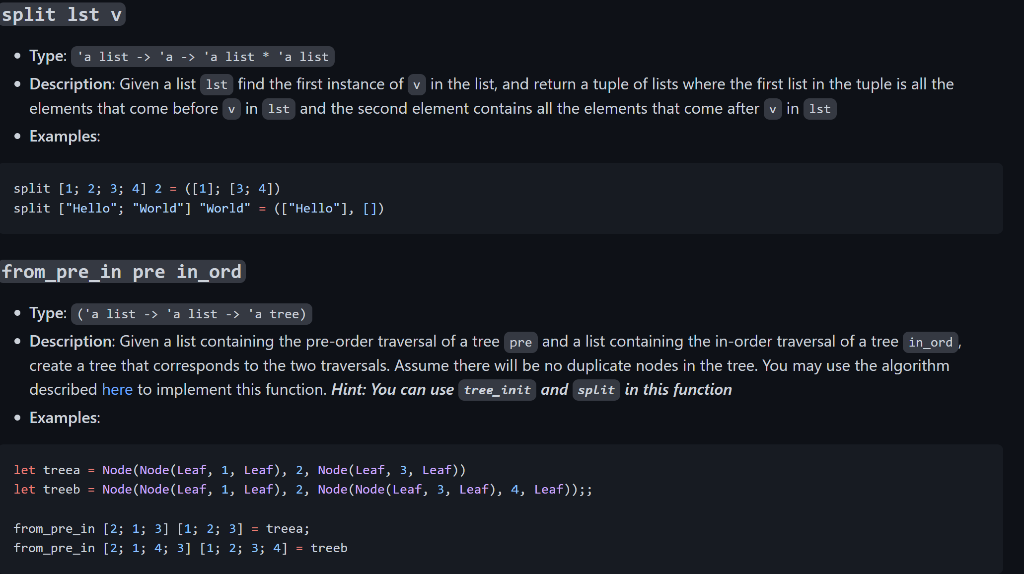
Given the type tree, please code the function from_pre_in that does what the description is asking for.

There are optional codes tree_init, split, and an optional type option, that may or may not be helpful in coding this function as helpers. If you choose to implement these two functions as well, please show the code as well. I have also provided a fold_tree method that might help in making the tree.

The only restriction to this code is that you can only use the stdlib module and List module libraries. You can use recursion and helpers for this function.

Please test to see that the code does what the example is showing:

let treea = Node(Node(Leaf, 1, Leaf), 2, Node(Leaf, 3, Leaf)) let treeb = Node(Node(Leaf, 1, Leaf), 2, Node(Node(Leaf, 3, Leaf), 4, Leaf));; from_pre_in [2; 1; 3] [1; 2; 3] = treea;; from_pre_in [2; 1; 4; 3] [1; 2; 3; 4] = treeb;;

Thank you.

type 'a tree = | Node of 'a tree *'a 'a 'a tree Leaf type 'a t= 'a option = None I Some of ' a let rec fold_tree fbt= match t with \( \begin{array}{l}\mid \text { Leaf } \\ \mid \text { Node }(l, v, r) ightarrow \text { let res_l }=\text { fold_tree } f b l \text { in } \\ \quad \text { let res_r } r=\text { fold_tree } f b r \text { in } \\ \quad f \text { res_l } v \text { res_r }\end{array} \) tree_init fv - Type: ('a ( ( a+b ' a ) option) ' a 'b tree) - Description: A generator f is a function that returns 3 values: v1,v2,v3. Using the definition of type option, f and an init value v, build a tree that has a root node with value v2 and a new generated left subtree with init value v1 and a new generated right subtree with init v3. If f returns None, a Leaf will be placed into the tree. - Examples: let generator 1a= if a