Question: When a reservoir is created by a new dam, 50 fish are introduced into the reservoir, which has an estimated carrying capacity of 8000 fish.

When a reservoir is created by a new dam, 50 fish are introduced into the reservoir, which has an estimated carrying capacity of 8000 fish. A logistic model of the fish population is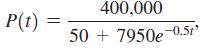 P(t) 400,000 50 + 7950e-0.5t where t is measured in years.

a. Graph P using a graphing utility. Experiment with different windows until you produce an S-shaped curve characteristic of the logistic model. What window works well for this function?

b. How long does it take for the population to reach 5000 fish? How long does it take for the population to reach 90% of the carrying capacity?c. How fast (in fish per year) is the population growing at t = 0? At t = 5?d. Graph P' and use the graph to estimate the year in which the population is growing fastest.

P(t) 400,000 50 + 7950e-0.5t

Step by Step Solution

★★★★★

3.36 Rating (162 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To graph the function Pt 400000507950e05t we can use a graphing utility such as Desmos or a graphi... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus 1st Questions!

Scientists often use the logistic growth function to model population growth, where P 0 is the initial population at time t = 0, K is the carrying capacity, and r 0 is the base growth rate. The...

In this activity, you will be evaluating whether you should purchase a hybrid car or its gasoline-engine counterpart. Select two car models that are similar, with one being a hybrid model and one...

Find the minimum cost 10 18 14 12 16

Two major themes from the introduction to module 4 are "Project Management" and "Managing Risk." Discuss, in depth, your analysis of the company's actions in relation to the concepts of these two...

Titanic: Project management - Lessons from history SDA Bod Introduction The White Star Line (WSL) was originally founded in Liverpool in 1845 by John Pilkington and Henry Wilson. The company's...

Financial crisis analysis. Find a current (within the last year) article on a company that has been faced with a significant financial crisis or challenge. It could be downsizing, starting up,...

0 Question 5 v B on pt \"0 2 Q 99 '3 Details Let yrt) represent your bank account balance, in dollars, after t years. Suppose you start with $30000 in the account. Each year the account earns 55%...

Question: Discuss the actions, decisions and strategies that were carried out by Stardust to ensure the success of introducing the Living Safety culture. (20 markah) note: please can you make at...

Situation Analysis Internal. Review factors within the company that are critical to the strategy of the firm, and classify them as strengths or weaknesses. Use a value chain analysis to determine...

Strategic Alternative Implementation Provide a complete and detailed analysis of the steps that must be taken to put the strategy into practice, including structural, leadership, control, incentive,...

#2 2) (3 points) Determine the voltage vc(t) across the capacitor for t 0 in the regime of critically damped response. 3) (3 points) Determine the voltage (t) across the inductor for t20 in the...

If x is a rational number and y is an irrational number, then A B C D Both x + y and xy are necessarily irrational Both x + y and xy are necessarily rational xy is necessarily irrational, but x + y...

14.57 Spam or junk emails are unsolicited messages sent in bulk through email (this process is also called spamming). To detect spam emails, we use a binary classification in which we give the label...

2. Give examples of when you have used passive, active, and interactive strategies to reduce your uncertainty in a new situation or before meeting a new person.

For the following exercises, find the domain of each function using interval notation. f(x) = 3x + 1 4x + 2 +2

For the following exercises, describe how the graph of the function is a transformation of the graph of the original function f. y = f(x) + 5

For the following exercises, determine whether the relation represents y as a function of x X= +5 7y-1

Some costs which give rise to future benefits cannot be directly associated with the revenues they generate. Such costs are allocated in a __________________ and _________________ manner to the...

The following materials standards have been established for a particular product: Standard quantity per unit of output 8.1 Pounds Standard price $15.10 per pound The following data pertain to...

Enter question here... Selected transactions for the Anthony Adams Company are presented in journal from below. Post the transactions to T accounts. Make one T account for each item and determine...