1. Treating year as the independent variable and the winning value as the dependent variable, find linear equations relating these variables (separately for men and women) using the data for the years 1992 and 1996. Compare the equations and comment on any similarities or differences.

2. Interpret the slopes in your equations from part 1. Do the y-intercepts have a reasonable interpretation? Why or why not?

3. Use your equations to predict the winning time in the 2004 Olympics. Compare your predictions to the actual results (2.18 hours for men and 2.44 hours for women). How well did your equations do in predicting the winning times?

4. Repeat parts 1 to 3 using the data for the years 1996 and 2000. How do your results compare?

5. Would your equations be useful in predicting the winning marathon times in the 2104 Summer Olympics? Why or why not?

Internet-based Project
Predicting Olympic Performance Measurements of human performance over time sometimes follow a strong linear relationship for reasonably short periods. In 2004 the Summer Olympic Games returned to Greece, the home of both the ancient Olympics and the first modern Olympics. The following data represent the winning times (in hours) for men and women in the Olympic marathon.

Transcribed Image Text:

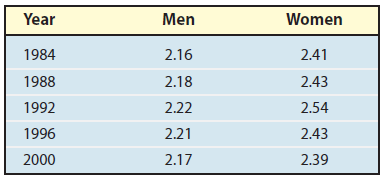
Year Men Women 1984 2.16 2.41 2.18 2.43 1988 2.22 1992 2.54 2.21 2.43 1996 2000 2.17 2.39