Question: (a) Considered the expression a n = (a n-1 ) 2 +Z , where z is some complex number (called the seed) and a 0

(a) Considered the expression a_n = (a_n-1)² +Z , where z is some complex number (called the seed) and a₀ = z. Compute a₁(=a²₀ + z), a₂(=a²₁ + z), a₃(=a²₂ + z), a₄, a₅ and a₆ for the following seeds: z₁ = 0.1 – 0.4i, z₂ = 0.5 + 0.8i, z₃ = -0.9 + 0.7i, z₄ = -1.1 + 0.1i, z₅ = 0 – 1.3i, and z₆ = 1 + 1i.

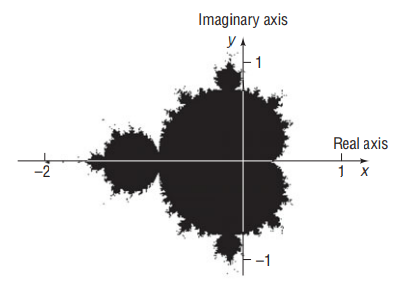
(b) The dark portion of the graph represents the set of all values z = x+ yi that are in the Mandelbrot set. Determine which complex numbers in part (a) are in this set by plotting them on the graph. Do the complex numbers that are not in the Mandelbrot set have any common characteristics regarding the values of found in part (a)?

(c) Compute |z| = √(x²+y²) for each of the complex numbers in part (a). Now compute |a₆| for each of the complex numbers in part (a). For which complex numbers is |a₆ ≤ |z| ≤ 2? Conclude that the criterion for a complex number to be in the Mandelbrot set is that |a_n| ≤ |z| and |z| ≤ 2.

Imaginary axis У -1 Real axis

Imaginary axis -1 Real axis

Step by Step Solution

★★★★★

3.38 Rating (173 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a b 9 a3 z do q 0104i 005048i 013035i 001 031i 05 08i 011 16i 205115i 33... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

1. For the expression (xy + z)x, let x = 2 and z = -7. Then multiply and simplify. 2. Explain two ways in which 12y - 722 and your answer to Exercise 42 are related. Use the words multiply and factor...

The Mann-Whitney L7 test is equivalent to the Wilcoxon rank-sum test for independent samples in the sense that it applies to the same situations and always leads to the same conclusions. In the...

A five-year follow-up study was carried out in a certain metropolitan area to assess the relationship of diet and weight to the incidence of stomach cancer. Data were obtained on n = 2,000 subjects....

Please, answer all the following questions: \f\f\f\f\f\f\f1.0 0.8 9.6 0.4 0.2 -2 N If you use MATLAB, here is a sample code. .Fourier preview clear all; n1=32; x=-5:0. 1 : 10; S=0 ; for k=0:1:n1 s=s...

Could someone review and assist 1-18 Home x | Mail - Darwish, Jacqueline - Out x DEL. 2-3 Mobius Problem Set: Modul x m Southern New Hampshire Unive x m Southern New Hampshire Unive x | Course Hero x...

At the end of this work you should submit a header file Complex.h, with the class interface, function declarations, and constexpr function definitions, and Complex.cpp that includes all the other...

there is also some starter code: complex.h : #ifndef COMPLEX_H #define COMPLEX_H #include using namespace std; /* YOUR TASK HERE IS TO GIVE THE COMPLETE DEFINITION OF THE class Complex AS DESCRIBED...

Solve problems 6,7,8,9, and 10 for me please. Amazing fact #9 (i) 6. Find the value of cos i + isin i and write it as a power of e. Complete the boxes with simplified numerators of ti or + 1. Powers...

cc170785fa926b2240534b10e7743155388d392a ID hours 1 37.09953814 2 34.58422938 3 37.85777106 4 36.03408777 5 38.71008438 6 38.18084857 7 37.7883698 8 38.41027533 9 39.53619743 10 37.46797595 11...

1 Data Analysis Assignment 4 Make sure you do the following. Points will be taken off if you do not. (For an example of formatting, see the sample solutions document posted in Blackboard.) 1.Type...

Calculate total interest expense that will be recorded on the books from January 2, 20X2, through December 31, 20X9 (assume zero interest expense during 20X1). The Corporation & Industry Financial...

Prove the following using a proof by contraposition: (a) Let x E Z; If x2 6x +5 is even, then x is odd. (b) If a product of two positive real numbers is greater than 100, then at least one of the...

SPY sells for $ 6 0 0 today and the risk - free rate of interest is 5 percent. A call and a put on SPY expire in three months and both options have an exercise price of $ 6 0 0 . If the put sells for...

2. State your position with regard to the choice between the single company-wide, cut-off rate versus the multiple divisional cut-off rates.

For the following exercises, find the magnitude and direction of the vector, 0

For the following exercises, find the area of the triangle with the given measurements. Round each answer to the nearest tenth. a = 7.2, b = 4.5, = 43

Write the complex number in polar form. 5 + 9i

I got 21.92-0.32 (xt-1) which is incorrect. can someone please provide the answers for all the questions with an explanation. thanks in advance The data below show the volume of transactions (in...

A company has an ROA of 6% and an equity multiplier of 2.0. Net Income for last year was $10.0 Million, of which $4.0 Million was paid out as dividends. What is the Sustainable Growth Rate? Select...

An assembly-line robot installs a CD player in each car produced on the line. For quality control, the units are tested to make sure that they are installed properly. The robot has a probability of...