A function defined by a power series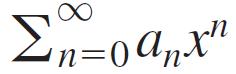

with a radius of convergence R > 0 has a Taylor series that converges to the function at every point of (-R, R). Show this by showing that the Taylor series generated by

is the series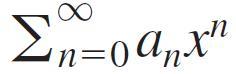 itself.

An immediate consequence of this is that series like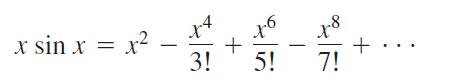

and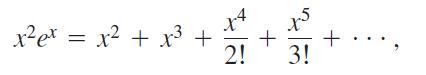

obtained by multiplying Taylor series by powers of x, as well as series obtained by integration and differentiation of convergent power series, are themselves the Taylor series generated by the functions they represent.

8 n=0an xn