a. Give an example of a differentiable function whose first derivative is zero at some point c even though has neither a local

a. Give an example of a differentiable function ƒ whose first derivative is zero at some point c even though ƒ has neither a local maximum nor a local minimum at c.

b. How is this consistent with Theorem 2? Give reasons for your answer.

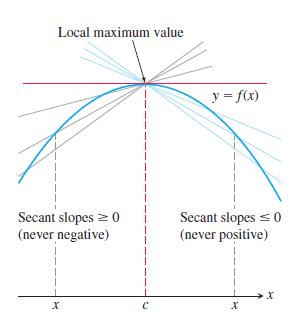
THEOREM 2-The First Derivative Theorem for Local Extreme Values If f has a local maximum or minimum value at an interior point c of its domain, and if f' is defined at c, then Proof To prove that f'(c) is zero at a local extremum, we show first that f'(c) cannot be positive and second that f'(c) cannot be negative. The only number that is neither posi- tive nor negative is zero, so that is what f'(c) must be. To begin, suppose that has a local maximum value at x = c (Figure 4.6) so that f(x) = f(c) 0 for all values of x near enough to c. Since c is an interior point of f's domain, f'(c) is defined by the two-sided limit Similarly, f'(c) = 0. f'(c) = lim x-c This means that the right-hand and left-hand limits both exist at x = c and equal f'(c). When we examine these limits separately, we find that f(x) = f(c) x - C lim: X-C f(x) = f(c) X C 0. Because (x-c) > 0 and f(x) f(c) (1)