a. Let a = x 0 < x 1 < x 2 < x n = b be any partition of [a,

a. Let a = x₀ 1 2 · · · n = b be any partition of [a, b], and let F be any antiderivative of ƒ. Show that

b. Apply the Mean Value Theorem to each term to show that F(x_i) - F(x_i-1) = ƒ(c_i)(x_i - x_i-1) for some c_i in the interval (x_i-1, x_i). Then show that F(b) - F(a) is a Riemann sum for ƒ on [a, b].

c. From part (b) and the definition of the definite integral, show that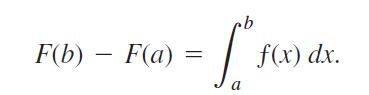

F(b) - F(a) = n [F(xi) - F(x-1)]. i=1