Although we are mainly interested in continuous functions, many functions in applications are piecewise continuous. A function (x) is piecewise continuous on a closed interval

Although we are mainly interested in continuous functions, many functions in applications are piecewise continuous. A function ƒ(x) is piecewise continuous on a closed interval I if ƒ has only finitely many discontinuities in I, the limits

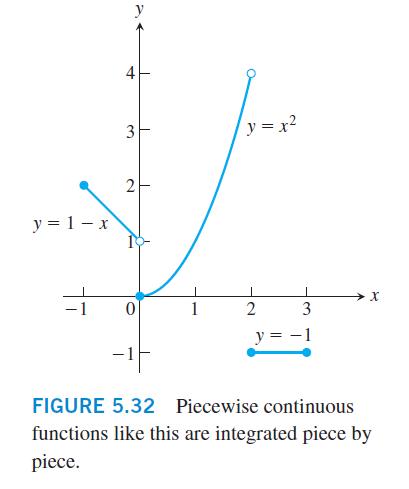
exist and are finite at every interior point of I, and the appropriate onesided limits exist and are finite at the endpoints of I. All piecewise continuous functions are integrable. The points of discontinuity subdivide I into open and half-open subintervals on which ƒ is continuous, and the limit criteria above guarantee that ƒ has a continuous extension to the closure of each subinterval. To integrate a piecewise continuous function, we integrate the individual extensions and add the results. The integral of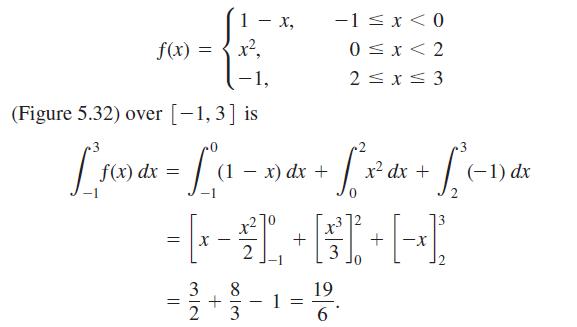

The Fundamental Theorem applies to piecewise continuous functions with the restriction that (d/dx)∫_a^x ƒ(t) dt is expected to equal ƒ(x) only at values of x at which ƒ is continuous. There is a similar restriction on Leibniz’s Rule.

Graph the function and integrate them over their domains.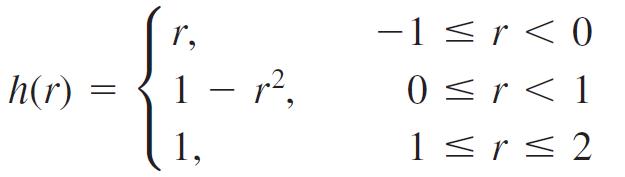

lim f(x) and lim f(x) x-c+*