At points on a circle of radius a, line segments are drawn perpendicular to the plane of the circle, the perpendicular at each point P being of length ks, where s is the length of the arc of the circle measured counterclockwise from (a, 0) to P and k is a positive constant, as shown here. Find the area of the surface formed by the perpendiculars along the arc beginning at (a, 0) and extending once around the circle.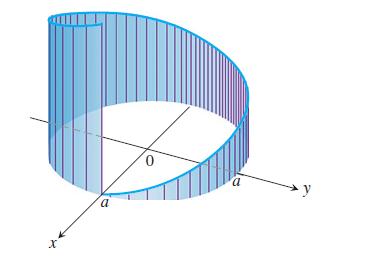

X a 0 a