Consider an n-sided regular polygon inscribed in a circle of radius r. Join the vertices of the polygon to the center of the circle, forming n congruent triangles (see figure).(a) Determine the central angle θ in terms of n.(b) Show that the area of each triangle is 1/2 r² sinθ.(c) Let A_n be the sum of the areas of the n triangles. Find lim _{n ∞} A_n.

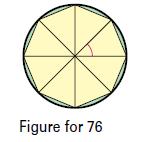
Figure for 76