Question: Consider the function defined by (a) Find fx(x, y) and fy(x, y) for (x, y) (0, 0). (b) Use the definition of partial derivatives

Consider the function defined by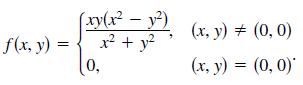f(x, y) = (xy(x - y) x + y 0, (x, y)


(a) Find fx(x, y) and fy(x, y) for (x, y) ≠ (0, 0).


(b) Use the definition of partial derivatives to find fx(0, 0) and fy(0, 0).


(c) Use the definition of partial derivatives to find fxy(0, 0) and fyx(0, 0).


(d) Using Theorem 13.3 and the result of part (c), what can be said about fxy or fyx?


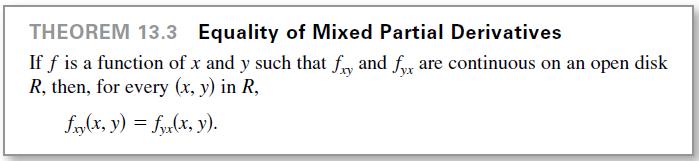
= (0,0) (x, y) = (0, 0)*

f(x, y) = (xy(x - y) x + y 0, (x, y) = (0,0) (x, y) = (0, 0)*

Step by Step Solution

★★★★★

3.41 Rating (160 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer
Step: 1 Unlock

a b f x 0 0 0 f y 0 0 0 c f x... View full answer

blur-text-image
Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock
Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Q:

Independent auditors must evaluate an entire set of financial statements. Considering that risk is always involved in selecting only a sample, why are auditors willing to accept less than a complete...

Q:

What can be said about the signs of the numbers a, b, and c in each case? (A) abc >0 (B) ab/c 0 (D) a2/bc

Q:

1. (a) Explain the meaning of the following interest rate concepts (short explanation): i. Spot-interest rate, 2p ii. Forward interest rate, 2p iii. Implicit forward interest rate, 2p iv....

Q:

I(x, y) = [ (2t + 1) esint dt + x Consider the function defined by - ( f(x, y) = xy(x-y x + y + 1 (2 0 (2t - 1) tan (t) dt (x, y) = (0,0) (x, y) = (0,0) (a) (8pt) Find f(x, y) and fy(x, y) for (x, y)...

Q:

Math for Econ I, Homework Assignment New York University Please write neat solutions for the problems below. Show all your work. If you only write the answer with no work, you will not be given any...

Q:

Infinite limit -- cusp or vertical tangent a) Consider the function f(x) defined as follows f(x) = x { fx) = cuberoot(x) } Find the derivative f(x) by the power rule and show f(x) is not defined at...

Q:

Non-Differentiability Corner Illustrate that the following function f(x) is not differentiable at x-2 due to a corner. - x2 + 4x +1 x

Q:

8. Find fx (x, y, z), fy ( x, y, z), fz ( x, y, z), fxx ( x, y, z), fyy ( x, y, z), fzz ( x, y, z), fxy (x, y, z), fxz (x, y, z), fyz (x, y, z) for the function f (x, y, z) = x3 - y2 + 24 + x3 y2z....

Q:

Hi, I need help with Calculus, take your time, thank you Below are the graphs of 6 functions A-F. There are also graphs of 5 derivative functions 1-5. Match each function with it's derivative. One...

Q:

Hi, I need help with my calculus homework, thank you! Take your time I appreciate the help :D Below are the graphs of 6 functions A-F. There are also graphs of 5 derivative functions 1-5. Match each...

Q:

Use the annual report of Carnival Corporation for the 2007 scal year to answer the following questions. This information can be found on either the annual report or the SEC 10-K filing at...

Q:

Morty's Original Business - Morty is a mortgage broker that provides a service, helping borrowers secure a mortgage loan from a lender. - Every loan that is secured is called a "closed loan", and...

Q:

You were considering buying a home with a 3 0 - year mortgage in 2 0 2 1 and could afford to make a down payment of $ 5 0 , 0 0 0 and up to $ 7 0 0 per month on mortgage payments. How much could you...

Q:

6. Which of the following stimuli do infants prefer to look at? a. Circles b. Colors c. Faces d. Machines

Q:

Use a double integral to find the volume of the indicated solid. X Improper integral Z Z= 1 (x + 1)(y + 1) 0x

Q:

Use a computer algebra system to find the mass and center of mass of the lamina bounded by the graphs of the equations for the given density. y = ln x, y = 0, x = 1, x = e, =k/x

Q:

Use a computer algebra system to find the mass and center of mass of the lamina bounded by the graphs of the equations for the given density. r = 2 cos 30, 6 TT 6' 0 - p = k

Q:

What is the name for a person who lends funds to a business entity and expects repayment with interest? a.owner b.proprietor c.stockholder d.creditor

Q:

CASE 4-2, PAGE 163, MANAGERIAL ACCOUNTING, 4TH EDITION, JAMES JIAMBALVO. MY EMAIL IS: arturo5532@hotmail.com THANKS

Q:

A bank statement shows a balance of $9,710 at June 30. A bank reconciliation is prepared and includes outstanding checks of $2,150, deposits in transit of $1,580, and a bank service charge of $50....