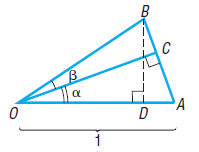
Geometry Refer to the figure. If |OA| = 1, show that: (a) Area OAC = 1/2 sin cos (b) Area OCB = 1/2

Geometry Refer to the figure. If |OA| = 1, show that: 

(a) Area ΔOAC = 1/2 sin α cos α

(b) Area ΔOCB = 1/2 |OB|² sin β cos β 

(c) Area ΔOAB = 1/2 |OB| sin(α + β)

(d) |OB| =  cos α/cos β

(e) sin(α + β) = sin α cos β + cos α sin β

C A D