How much work would it take to pump oil from the tank in Example 5 to the level of the top of the tank if the tank were completely full?

In Example 5

In Figure 6.39

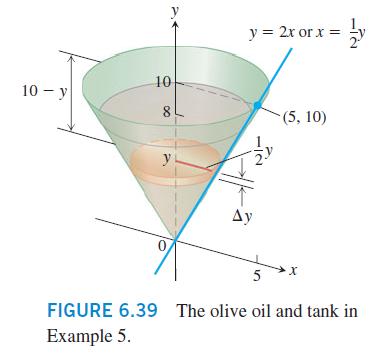
EXAMPLE 5 The conical tank in Figure 6.39 is filled to within 2 ft of the top with olive oil weighing 57 lb/ft. How much work does it take to pump the oil to the rim of the tank? We imagine the oil divided into thin slabs by planes perpendicular to the y-axis at the points of a partition of the interval [0,8]. The typical slab between the planes at y and y + Ay has a volume of about 2 AV = (radius) (thickness) = (y) ay = y ay ft. The force F(y) required to lift this slab is equal to its weight, F(y) = 57 AV = 57my2 Ay lb. The distance through which F(y) must act to lift this slab to the level of the rim of the cone is about (10-y) ft, so the work done lifting the slab is about AW = 57 (10-y)y Ay ft-lb. Assuming there are n slabs associated with the partition of [0, 8], and that y = y denotes the plane associated with the kth slab of thickness Ay, we can approximate the work done lifting all of the slabs with the Riemann sum W = 57 (10-Ay; ft-lb. The work of pumping the oil to the rim is the limit of these sums as the norm of the parti- tion goes to zero and the number of slabs tends to infinity: W = lim T - $ 57 (10 vi Ay * 577 (10 y)y dy = - 577 = Weight (weight per unit volume) x volume =: 8 (10y - y) dy 57 103 1478 Jo 30,561 ft-lb.