Suppose that, instead of being full, the tank in Example 5 is only half full. How much work does it take to pump the remaining oil to a level 4 ft above the top of the tank?

Example 5

In Figure 6.39

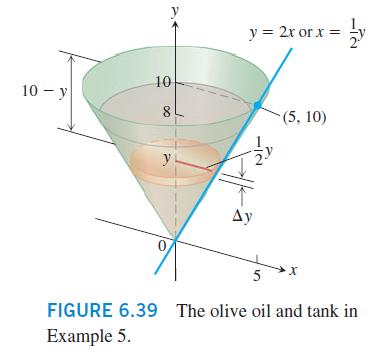
EXAMPLE 5 The conical tank in Figure 6.39 is filled to within 2 ft of the top with olive oil weighing 57 lb/ft. How much work does it take to pump the oil to the rim of the tank? We imagine the oil divided into thin slabs by planes perpendicular to the y-axis at the points of a partition of the interval [0,8]. The typical slab between the planes at y and y + Ay has a volume of about AV = 7(radius) (thickness) = (y + The force F(y) required to lift this slab is equal to its weight, F(y) = 57 AV = 57 y Ay lb. Ay = 57 5 (10-yy: Ay, ft-lb. The distance through which F(y) must act to lift this slab to the level of the rim of the cone is about (10 - y) ft, so the work done lifting the slab is about AW = 57 (10-y)y Ay ft-lb. Assuming there are n slabs associated with the partition of [0, 8], and that y = y denotes the plane associated with the kth slab of thickness Ay, we can approximate the work done lifting all of the slabs with the Riemann sum W - 577 = y Ay ft. The work of pumping the oil to the rim is the limit of these sums as the norm of the parti- tion goes to zero and the number of slabs tends to infinity: W = lim = Weight = (weight per unit volume) x volume 577 (10 - My Aye - 577 (10 - y)y dy = 57 103 8 (10y - y3) dy 1478 Jo 30,561 ft-lb.