In calculus you will learn that, if

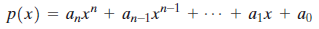
is a polynomial function, then the derivative of P(x) is

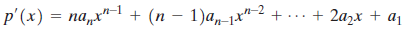
Newton's Method is an efficient method for approximating the x-intercepts (or real zeros) of a function, such as p(x). The following steps outline Newton's Method.

STEP 1: Select an initial value that is somewhat close to the x-intercept being sought.

STEP 2: Find values for x using the relation

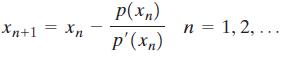
until you get two consecutive values x_n and x_n+1 that agree to whatever decimal place accuracy you desire.

STEP 3: The approximate zero will be x_n+1.

Consider the polynomial p(x) = x³ - 7x - 40.

(a) Evaluate p(5) and p(-3).

(b) What might we conclude about a zero of p? Explain.

(c) Use Newton's Method to approximate an x-intercept, r, -3

(d) Use a graphing utility to graph p(x) and verify your answer in part (c).

(e) Using a graphing utility, evaluate p(r) to verify your result.

() %3D ," + ,-1x"-1 +. + ajx + ao '() (x) %3D , "-1 + ( 1), *"-2 + 2z + j