Question: In parts (a)(h), prove the property for vector fields F and G and scalar function f. (Assume that the required partial derivatives are continuous.) (a)

In parts (a)–(h), prove the property for vector fields F and G and scalar function f. (Assume that the required partial derivatives are continuous.)

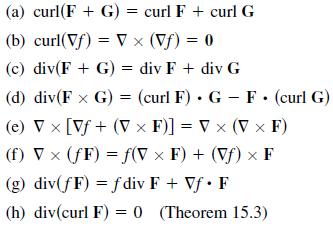
(a) curl(F + G) = curl F + curl G (b) curl(vf)

= V (Vf) = 0 (c) div(F + G) = div F

(a) curl(F + G) = curl F + curl G (b) curl(vf) = V (Vf) = 0 (c) div(F + G) = div F + div G (d) div(F x G) = (curl F) G - F. (curl G) (e) x [Vf+ (V x F)] = V (V x F) (f) x (fF) = f(V x F) + (vf) F (g) div(fF) = f div F + Vf. F (h) div(curl F) = 0 (Theorem 15.3)

Step by Step Solution

★★★★★

3.39 Rating (158 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a To prove curlFG curl F curl G we can use the properties of the curl and the product rule for taking derivatives Let F P i Q j R k and G U i V j W k be vector fields The curl of F is given by curl F ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Precalculus Questions!

Managing Scope Changes Case Study Scope changes on a project can occur regardless of how well the project is planned or executed. Scope changes can be the result of something that was omitted during...

Prove the property for all integers r and n, where 0 r n. 1. nCr = nCn-r 2. nC0 - nC1 3. n+1Cr = nCr + nCr-1 4. The sum of the numbers in the nth row of Pascal's Triangle is 2n.

Prove that is continuous on R2 and has first-order partial derivatives everywhere on R2, but f is not differentiable at (0, 0). (x, y)(0.0) (x, y) = (0,0) f(x, y) = X2 +y2 0

77. Proof In parts (a), (b), (c), (d), (e), (f), (9), and (h), prove the property for vector fields F and G and scalar function f. (Assume that the required partial derivatives are continuous.) a....

1. Prove the given properties for the vector fields F and G, scalar c, and scalar function f. Assume that the required partial derivatives are continuous. (a) V . (cF) = cV . F. . ( D+ 1 ) . A ( q )...

Prove (a) - (d) vector differential identities Vector differential identities. Let f and g be scalar valued functions from R' to R and F and G be vector fields from R' to RS. Assuming that all...

(iii) Now express your decision rule instead using only the quantities p(Ck), p(Cj ), p(x|Ck), p(x|Cj ), and relate it to the diagram above. [2 marks] (iv) If the classifier decision rule assigns...

Sodium metal requires a photon with a minimum energy of 4.41 10-19J to emit electrons. (a) What is the minimum frequency of light necessary to emit electrons from sodium via the photoelectric...

The Max- Min theorem states that: 1) If f has neither an absolute Max nor an absolute Min on [a, b], then f is not continuous on [a,b] 2) fis continuous on [a, b], iff f has an absolute Max and an...

Locate and read through Form 8 8 6 7 , Paid Preparer s Due Diligence Checklist, found in the Supporting Materials section. You will be asked to specifically address items on the form and to expand on...

By choosing to speak from the fl oor instead of the dais, a speaker can show the audience a sense of: (a) respect (b) closeness (c) equality (d) informality

Test for symmetry with respect to each axis and to the origin. y = x - x

Find the slope and the -intercept (if possible) of the line. x + 5y = 20

Test for symmetry with respect to each axis and to the origin. y = x - 6

for part b, in the blue box put either 'increased' or 'decreased' The spreadsheet below has data on Microsoft and the S&P 500 from 1986 to 2006. Complete the steps below using cell references to...

A credit sale is made on July 10 for $900 terms 2/10 , n / 30, On July 12. $100 of goods are returned for credit. Give the journal entry on July 19 to record the receipt of the balance due within the...

Question 1 of 1 Which of the following are relevant in short-term decision making? Select the correct answer(s). Multiple boxes may be checked if needed. Purchase price of new equipment Reduction in...