In submarine location problems, it is often necessary to find a submarine’s closest point of approach (CPA) to a sonobuoy (sound detector) in the water. Suppose that the submarine travels on the parabolic path y = x² and that the buoy is located at the point (2, -1/2).

a. Show that the value of x that minimizes the distance between the submarine and the buoy is a solution of the equation x = 1/(x² + 1).

b. Solve the equation x = 1/(x² + 1) with Newton’s method.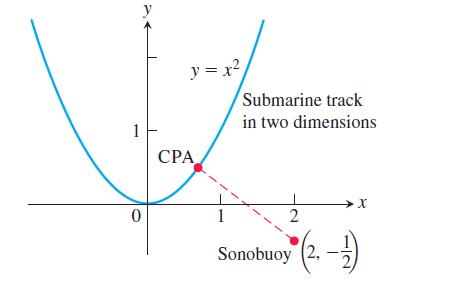

1 y 0 y = x/ CPA 1 Submarine track in two dimensions 2 X Sonobuoy (2, (2, -1/-)