Integration by parts leads to a rule for integrating inverses that usually gives good results: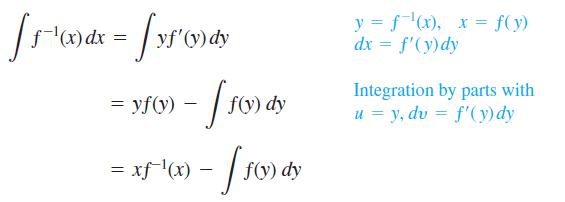

The idea is to take the most complicated part of the integral, in this case ƒ ^-1(x), and simplify it first. For the integral of ln x, we get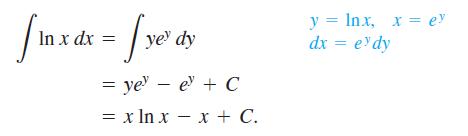

For the integral of cos^-1 x we get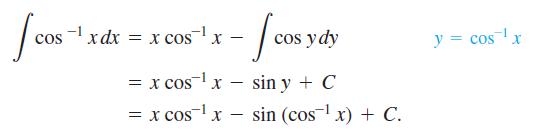

Use the formula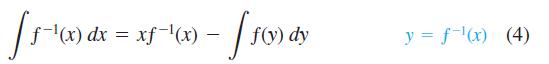

to evaluate the integrals. Express your answers in terms of x.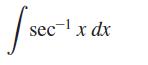

[1(x) dx = [yf'(y) dy f(y) ) dy = yf(y) - [6). = xf '(x) - [ f(1) dy y = f(x), x = f(y) dx = f'(y) dy Integration by parts with u = y, du = f'(y) dy