Let T(t, x, y, z) be a function with continuous second derivatives giving the temperature at time t at the point (x, y, z) of a solid occupying a region D in space. If the solid’s heat capacity and mass density are denoted by the constants c and r, respectively, the quantity cρT is called the solid’s heat energy per unit volume.

a. Explain why -∇T points in the direction of heat flow.

b. Let -k∇T denote the energy flux vector. (Here the constant k is called the conductivity.) Assuming the Law of Conservation of Mass with -k∇T = v and cρT = p in Exercise 31, derive the diffusion (heat) equation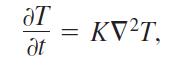

where K = k/(cρ) > 0 is the diffusivity constant.

Data from Exercise 31

Let v(t, x, y, z) be a continuously differentiable vector field over the region D in space and let p(t, x, y, z) be a continuously differentiable scalar function. The variable t represents the time domain. The Law of Conservation of Mass asserts that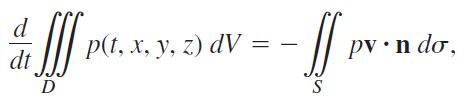

where S is the surface enclosing D.

at = KVT,